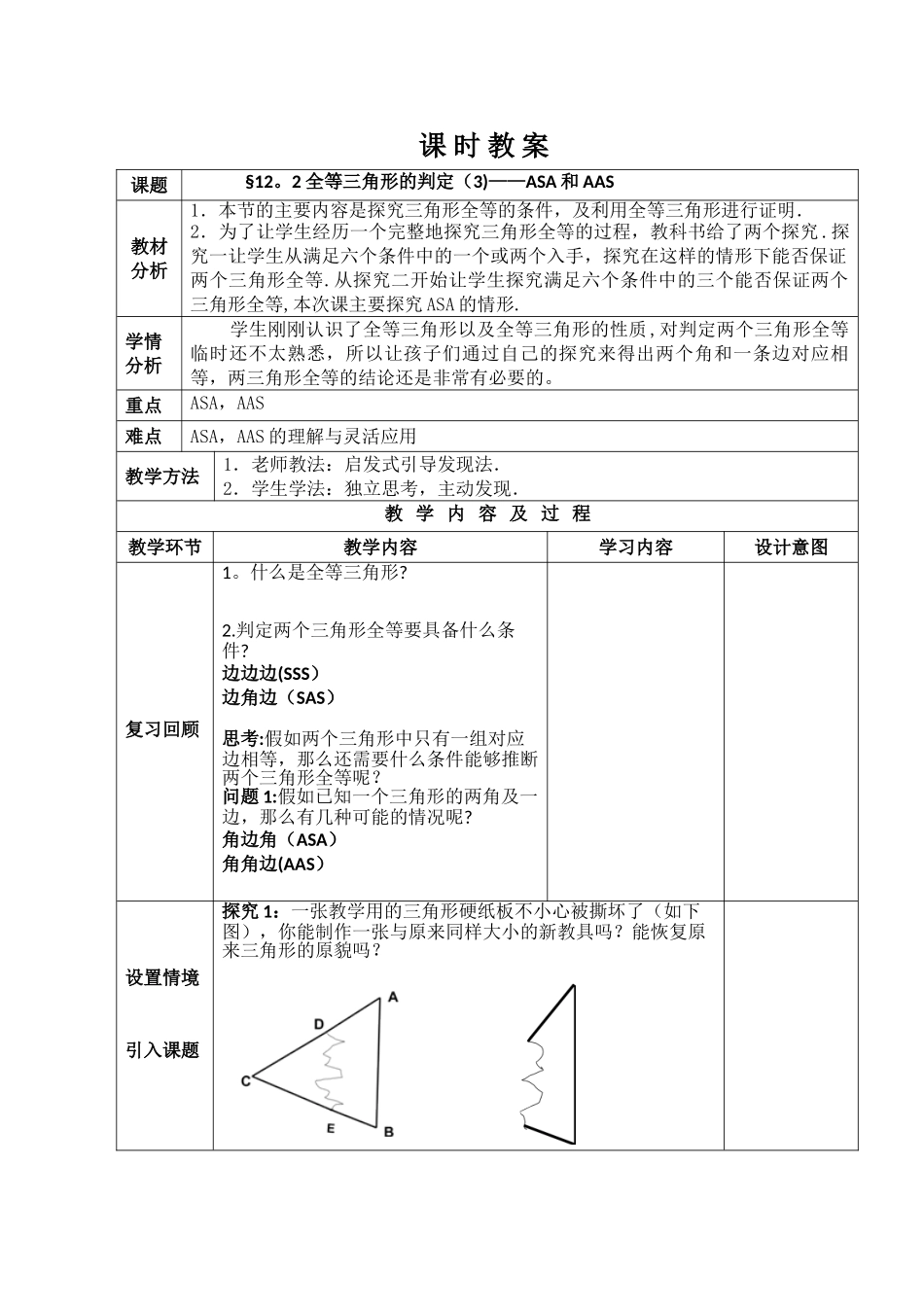
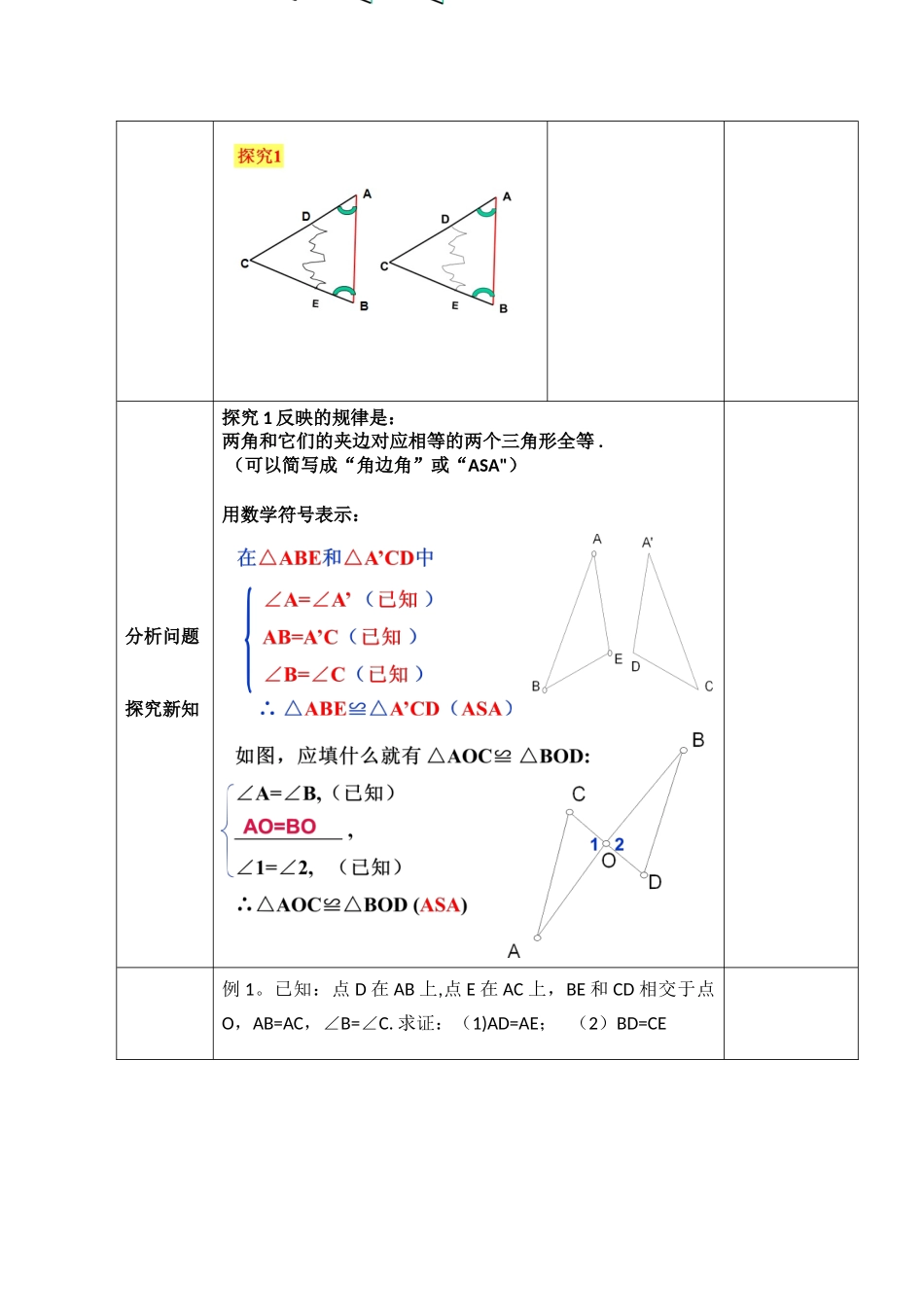
课 时 教 案课题 §12。2 全等三角形的判定(3)——ASA 和 AAS教材分析1.本节的主要内容是探究三角形全等的条件,及利用全等三角形进行证明.2.为了让学生经历一个完整地探究三角形全等的过程,教科书给了两个探究 .探究一让学生从满足六个条件中的一个或两个入手,探究在这样的情形下能否保证两个三角形全等.从探究二开始让学生探究满足六个条件中的三个能否保证两个三角形全等,本次课主要探究 ASA 的情形.学情分析 学生刚刚认识了全等三角形以及全等三角形的性质,对判定两个三角形全等临时还不太熟悉,所以让孩子们通过自己的探究来得出两个角和一条边对应相等,两三角形全等的结论还是非常有必要的。重点ASA,AAS难点ASA,AAS 的理解与灵活应用教学方法1.老师教法:启发式引导发现法.2.学生学法:独立思考,主动发现.教 学 内 容 及 过 程教学环节教学内容学习内容设计意图复习回顾1。什么是全等三角形?2.判定两个三角形全等要具备什么条件?边边边(SSS) 边角边(SAS)思考:假如两个三角形中只有一组对应边相等,那么还需要什么条件能够推断两个三角形全等呢?问题 1:假如已知一个三角形的两角及一边,那么有几种可能的情况呢?角边角(ASA) 角角边(AAS)设置情境引入课题探究 1:一张教学用的三角形硬纸板不小心被撕坏了(如下图),你能制作一张与原来同样大小的新教具吗?能恢复原来三角形的原貌吗?分析问题探究新知 分析问题探究新知探究 1 反映的规律是:两角和它们的夹边对应相等的两个三角形全等 . (可以简写成“角边角”或“ASA")用数学符号表示:例 1。已知:点 D 在 AB 上,点 E 在 AC 上,BE 和 CD 相交于点O,AB=AC,∠B=∠C. 求证:(1)AD=AE; (2)BD=CE 举一反三巩固新知练习 1:已知:如图,∠1=∠2,∠3=∠4 求证:AC=AD探究 2:如下图,在△ABC 和△DEF 中,∠A =∠D, ∠ B=∠E, BC=EF, △ABC 与△DEF 全等吗?能利用角边角条件证明你的结论吗?证明:在△ABC 和△DEF 中,∠A +∠B +∠C=1800, ∠D +∠E +∠F =1800, ∠A =∠D, ∠B=∠E, ∴ ∠C=∠F, ∴ ∠B=∠E, BC=EF, ∠C=∠F, ∴ △ABC ≌△DEF (ASA)探究 2 反映的规律是:两个角和其中一个角的对边对应相等的两个三 角 形 全 等 ( 可 以 简 写 成 “ 角 角 边 ” 或“AAS")用数学符号表示:例 2: 如图,O 是 AB 的中点,∠A= ∠B, △AOC与...