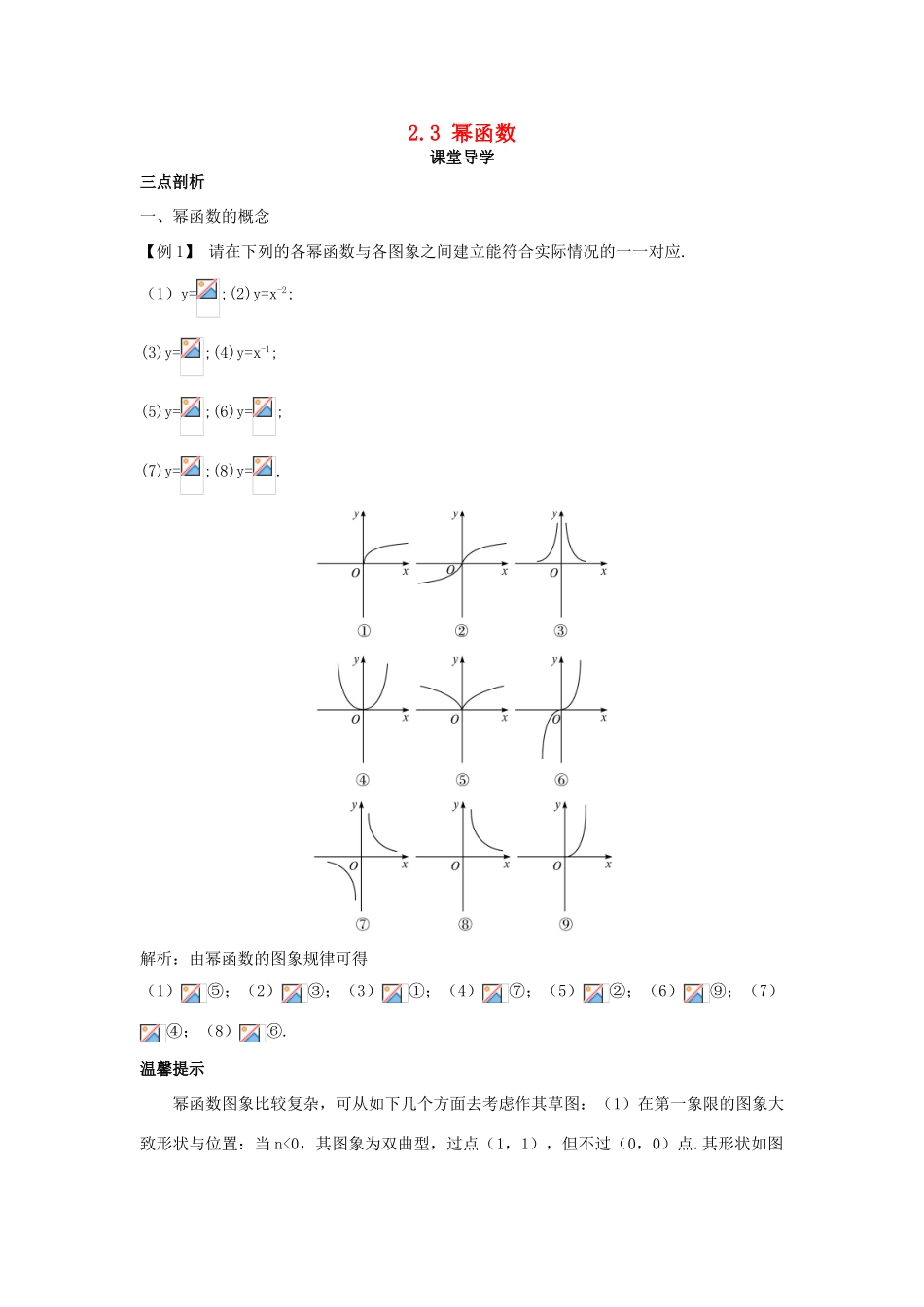
2.3 幂函数课堂导学三点剖析一、幂函数的概念【例 1】 请在下列的各幂函数与各图象之间建立能符合实际情况的一一对应.(1)y=;(2)y=x-2;(3)y=;(4)y=x-1;(5)y=;(6)y=;(7)y=;(8)y=.解析:由幂函数的图象规律可得(1)⑤;(2)③;(3)①;(4)⑦;(5)②;(6)⑨;(7)④;(8)⑥.温馨提示 幂函数图象比较复杂,可从如下几个方面去考虑作其草图:(1)在第一象限的图象大致形状与位置:当 n<0,其图象为双曲型,过点(1,1),但不过(0,0)点.其形状如图①所示;当 01 时图象为抛物线型,过(0,0),(1,1)两点,其形状如图④所示. (2)图象在第一象限的排队情况,在 x=1 的右侧,沿箭头的方向,幂指数逐渐减小.如图:【例 2】比较大小:(1)____________;(2)0.71.5_____________________0.61.5;(3)_____________;(4)0.15-1.2_____________0.17-1.2;(5)0.20.6_____________________0.30.4;(6)_______________.解析:(1)—(4)可直接应用幂函数的单调性比较大小.(1)<;(2)>;(3)<;(4)>. 由于(5)(6)中的两数的底数和指数均不相同,需借助“中间量”,同时利用幂函数和指数函数的单调性比较大小. (5)0.20.6<0.30.6<0.30.4;(6)=<<.答案:(1)< (2)> (3)< (4)> (5)< (6)<温馨提示 利用幂函数的单调性比较两个函数值的大小一般有如下三种情况: (1)同指数,不同底,可用幂函数的单调性直接比较大小. (2)同底不同指数的,可用幂函数图象的排队情况进行比较. (3)不同底,不同指数的,有时需要引入“中间量”进行比较.二、幂函数的图象和性质【例 3】函数 f(x)=(m2-m-1)是幂函数,且在 x∈(0,+∞)上是减函数,则实数 m 的取值集合是( )A.{m|m=-1 或 m=2} B.{m|-1