2.2.3线面平行的性质(廖丽微)

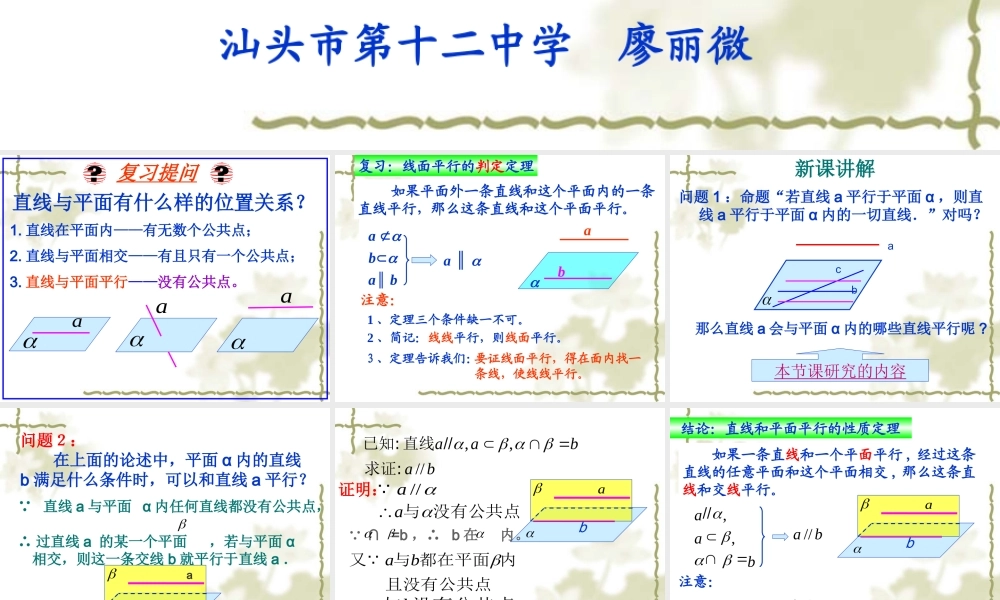
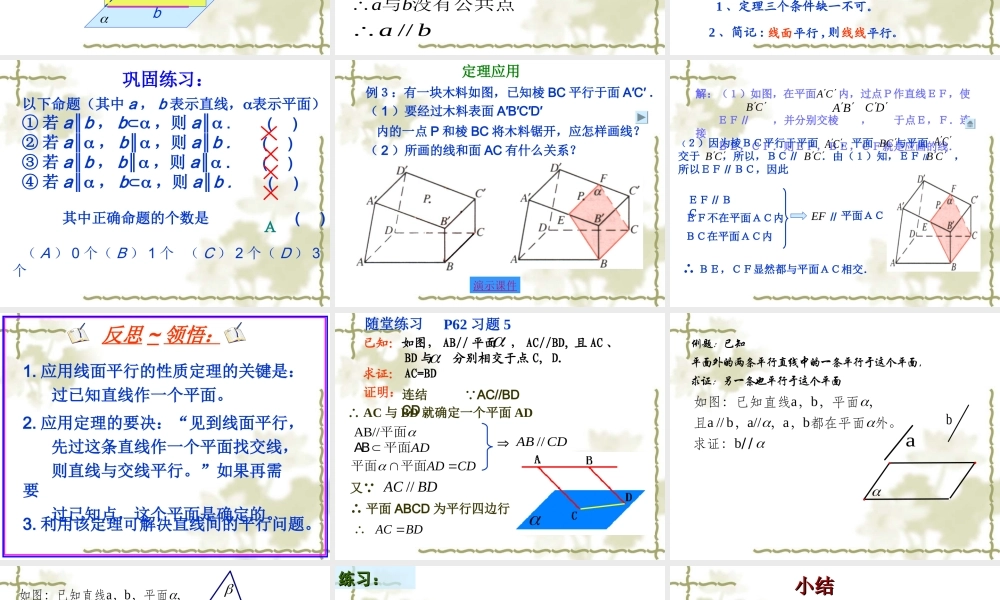
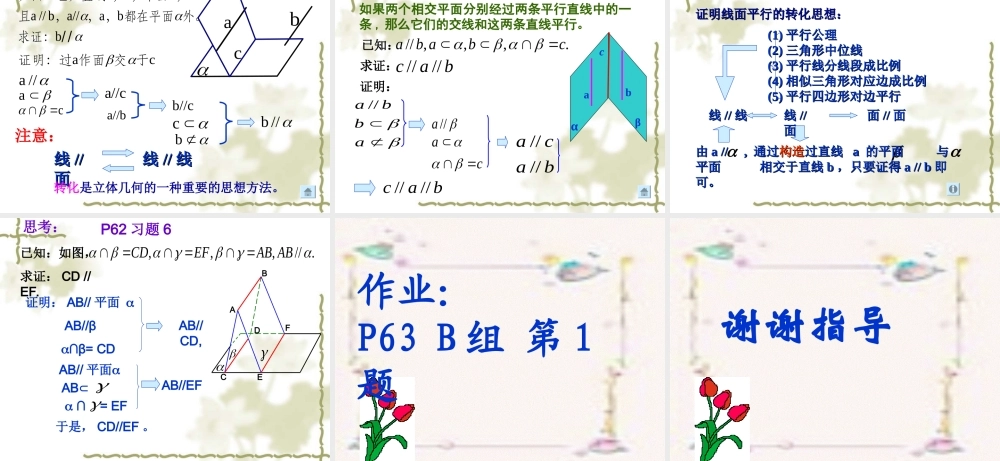
汕头市第十二中学 廖丽微 复习提问直线与平面有什么样的位置关系？aa1. 直线在平面内——有无数个公共点；2. 直线与平面相交——有且只有一个公共点；3. 直线与平面平行——没有公共点。a 复习：线面平行的判定定理 如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。baba ∥ ba a ∥ 注意：1 、定理三个条件缺一不可。2 、简记：线线平行，则线面平行。3 、定理告诉我们：要证线面平行，得在面内找一条线，使线线平行。 新课讲解问题 1 ：命题“若直线 a 平行于平面 α ，则直 线 a 平行于平面 α 内的一切直线．”对吗？ abc本节课研究的内容那么直线 a 会与平面 α 内的哪些直线平行呢 ? 问题２： 在上面的论述中，平面 α 内的直线b 满足什么条件时，可以和直线 a 平行？ 直线 a 与平面 α 内任何直线都没有公共点， ∴ 过直线 a 的某一个平面 ，若与平面 α 相交，则这一条交线 b 就平行于直线 a ．ba ,,//aabab 已知: 直线求证:证明：//aa 与 没有公共点ab 与 没有公共点ab又与 都在平面 内 且没有公共点//abba ∩ =b ，∴ b 在 内。 结论：直线和平面平行的性质定理 如果一条直线和一个平面平行 , 经过这条直线的任意平面和这个平面相交 , 那么这条直线和交线平行。注意：1 、定理三个条件缺一不可。2 、简记 : 线面平行 , 则线线平行。baba //,,aab    巩固练习： 以下命题（其中 a ， b 表示直线，表示平面）① 若 a∥b ， b ，则 a∥ . ( ) ② 若 a∥ ， b∥ ，则 a∥b . ( ) ③ 若 a∥b ， b∥ ，则 a∥ . ( ) ④ 若 a∥ ， b ，则 a∥b . ( ) 其中正确命题的个数是 ( ) （ A ） 0 个（ B ） 1 个 （ C ） 2 个（ D ） 3个 Ａ 例３：有一块木料如图，已知棱 BC 平行于面 A′C′ ．（ 1 ）要经过木料表面 A′B′C′D′ 内的一点 P 和棱 BC 将木料锯开，应怎样画线？（ 2 ）所画的线和面 AC 有什么关系？演示课件定理应用 CACBBADC解：（１）如图，在平面 内，过点Ｐ作直线ＥＦ，使 ＥＦ // ，并分别交棱 ， 于点Ｅ，Ｆ．连接 ＢＥ，ＣＦ．则ＥＦ，ＢＥ，ＣＦ就是应画的线．...