（江苏专版）中考数学一轮复习 第四章 图形的认识 4.5 特殊的平行四边形（试卷部分）课件-人教版初中九年级全册数学课件

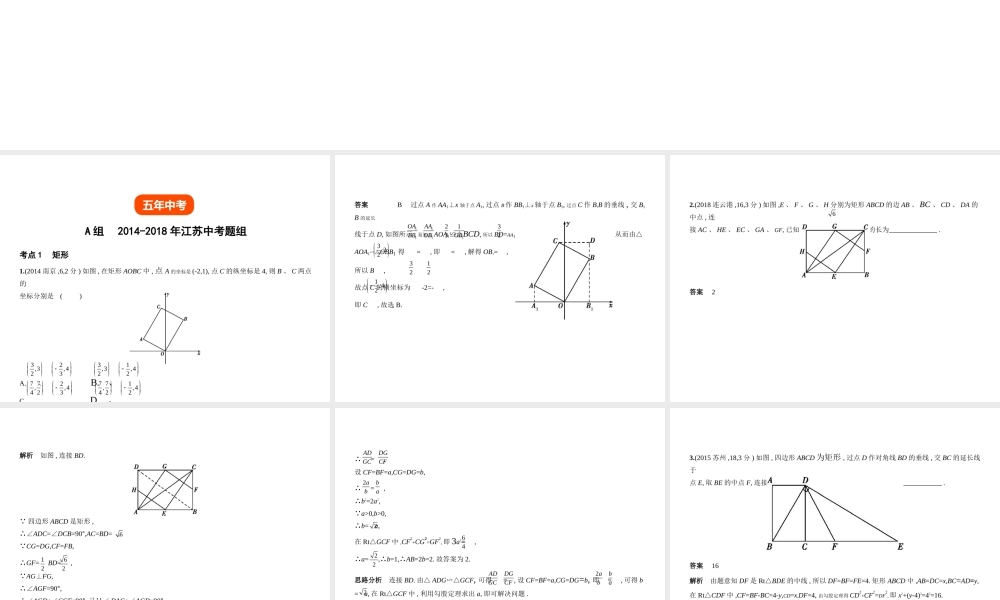
§4.5 特殊的平行四边形中考数学 ( 江苏专用 )考点 1 矩形A 组 2014-2018 年江苏中考题组五年中考1.(2014 南京 ,6,2 分 ) 如图 , 在矩形 AOBC 中 , 点 A 的坐标是 (-2,1), 点 C 的纵坐标是 4, 则 B 、 C 两点的坐标分别是 ( ) A. 、 B. 、 C. 、 D. 、 3 ,322 ,433 ,321 ,427 7,4 22 ,437 7,4 21 ,42答案 B 过点 A 作 AA1⊥x 轴于点 A1, 过点 B 作 BB1⊥x 轴于点 B1, 过点 C 作 B1B 的垂线 , 交 B1B 的延长线于点 D, 如图所示 , 易知△ AOA1≌△BCD, 所以 BD=AA1=1, 故点 B 的纵坐标是 4-1=3, 从而由△AOA1∽△OBB1 得 = , 即 = , 解得 OB1= ,所以 B ,故点 C 的横坐标为 -2=- ,即 C , 故选 B.11OABB11AAOB2311OB323 ,3232121 ,422.(2018 连云港 ,16,3 分 ) 如图 ,E 、 F 、 G 、 H 分别为矩形 ABCD 的边 AB 、 BC 、 CD 、 DA 的中点 , 连接 AC 、 HE 、 EC 、 GA 、 GF, 已知 AG⊥GF,AC= , 则 AB 的长为 . 6答案 2解析 如图 , 连接 BD. 四边形 ABCD 是矩形 ,∴∠ADC=∠DCB=90°,AC=BD= , CG=DG,CF=FB,∴GF= BD= , AG⊥FG,∴∠AGF=90°,∴∠AGD+∠CGF=90°, 又 ∠ DAG+∠AGD=90°,∴∠DAG=∠CGF,∴△ADG∽△GCF,61262∴ = ,设 CF=BF=a,CG=DG=b,∴ = ,∴b2=2a2, a>0,b>0,∴b= a,在 Rt△GCF 中 ,CF2+CG2=GF2, 即 3a2= ,∴a= ,∴b=1,∴AB=2b=2. 故答案为 2.ADGCDGCF2abba26422思路分析 连接 BD. 由△ ADG∽△GCF, 可得 = , 设 CF=BF=a,CG=DG=b, 即 = , 可得 b= a, 在 Rt△GCF 中 , 利用勾股定理求出 a, 即可解决问题 .ADGCDGCF2abba2解题关键 本题考查中点四边形、矩形的性质、相似三角形的判定和性质、勾股定理等知识 , 解题的关键是综合运用所学知识 , 连接对角线 , 运用相似、勾股定理列出方程解决问题 .3.(2015 苏州 ,18,3 分 ) 如图 , 四边形 ABCD 为矩形 , 过点 D 作对角线 BD 的垂线 , 交 BC 的延长线于点 E, 取 BE 的中点 F, 连接 DF,DF=4. 设 AB=x,AD=y, 则 x2+(y-4)2 的值为 . 答案 16解析 由题意知 DF 是 Rt△BDE 的中线 ,...