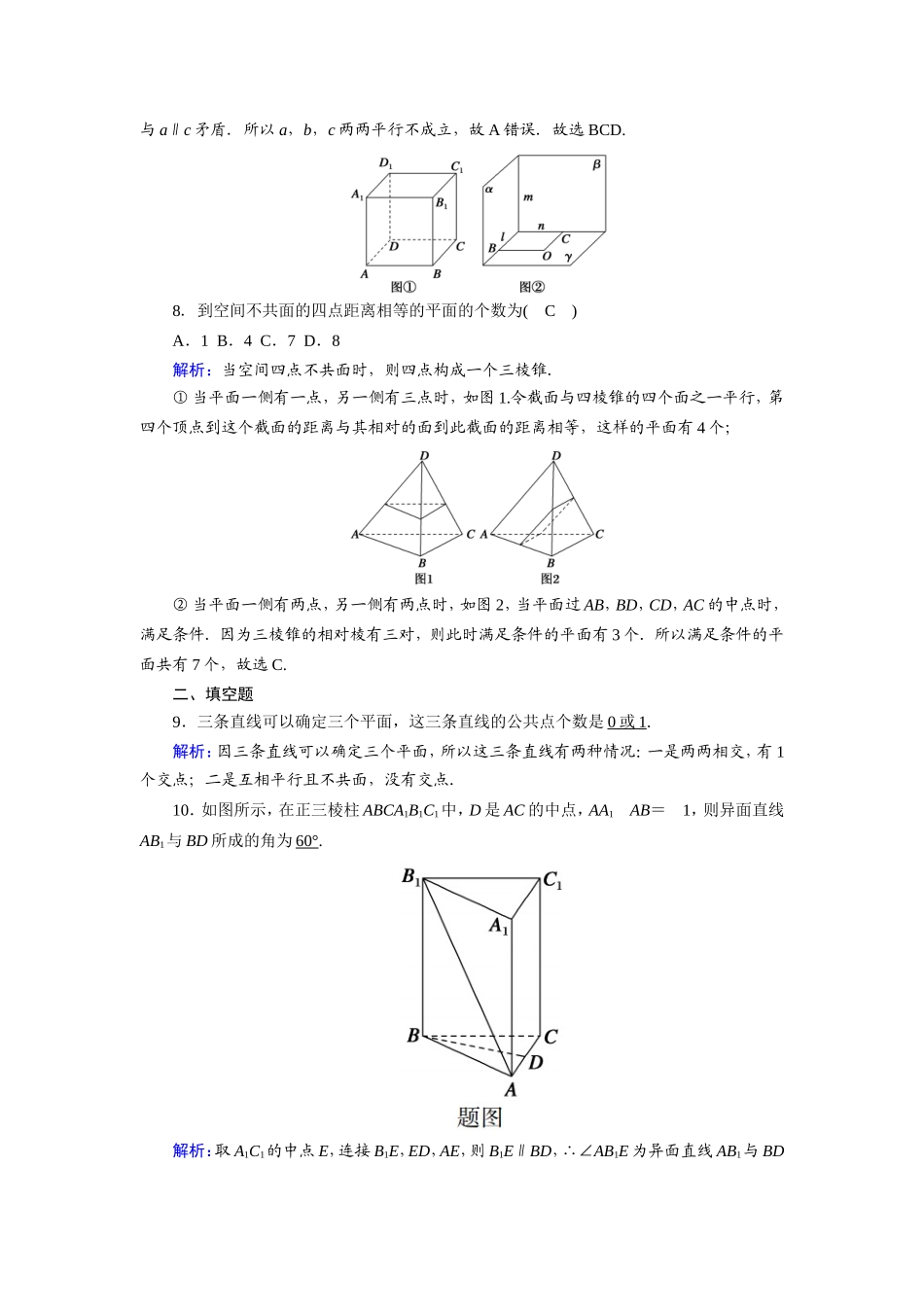
课时作业42空间点、直线、平面之间的位置关系一、选择题1.给出下列命题:①经过三点确定一个平面;②梯形可以确定一个平面;③两两相交的三条直线最多可以确定三个平面;④如果两个平面有三个公共点,则这两个平面重合.其中正确命题的个数是(C)A.0B.1C.2D.3解析:对于①,未强调三点不共线,故①错误;②正确;对于③,三条直线两两相交,如空间直角坐标系,能确定三个平面,故③正确;对于④,未强调三点不共线,则这两个平面也可能相交,故④错误.故选C.2.在正方形ABCDA1B1C1D1中,棱所在的直线与直线BA1是异面直线的条数是(C)A.4B.5C.6D.7解析:如图,在正方体ABCDA1B1C1D1中,直线BA1⊂平面ABB1A1,则有AD,B1C1,CD,C1D1,CC1,DD1,共6条直线与BA1是异面直线,故选C.3.已知a,b,c是两两不同的三条直线,则下面四个命题中,为真命题的是(C)A.若直线a,b异面,b,c异面,则a,c异面B.若直线a,b相交,b,c相交,则a,c相交C.若a∥b,则a,b与c所成的角相等D.若a⊥b,b⊥c,则a∥c解析:若直线a,b异面,b,c异面,则a,c可能相交、平行或异面;若a,b相交,b,c相交,则a,c可能相交、平行或异面;若a⊥b,b⊥c,则a,c可能相交、平行或异面;由异面直线所成的角的定义知选项C中的命题为真.故选C.4.已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是(D)A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面解析:因为直线a与平面α,β的位置关系不确定,则直线b和c的位置关系可能是相交、平行或异面,故选D.5.如图所示,在四面体ABCD中,若直线EF和GH相交,则它们的交点一定(A)A.在直线DB上B.在直线AB上C.在直线CB上D.以上都不对解析:设直线EF与GH的交点为M. EF⊂平面ABD,GH⊂平面CBD,∴M∈平面ABD,且M∈平面CBD.又 平面ABD∩平面CBD=BD,∴M∈BD,∴EF与GH的交点在直线DB上.6.在正四棱锥PABCD中,PA=2,直线PA与平面ABCD所成的角为60°,E为PC的中点,则异面直线PA与BE所成的角为(C)A.90°B.60°C.45°D.30°解析:连接AC,BD交于点O,连接OE,OP,则O是AC,BD的中点,又E是PC的中点,∴OE∥AP,∴∠OEB为异面直线PA与BE所成的角(或补角). 四棱锥PABCD是正四棱锥,∴PO⊥平面ABCD,则∠PAO为直线PA与平面ABCD所成的角,即∠PAO=60°.又PA=2,∴OA=OB=1,OE=1,∴在Rt△OBE中,∠OEB=45°,即异面直线PA与BE所成的角为45°,故选C.7.(多选题)已知平面α,β,γ两两垂直,直线a,b,c满足a⊂α,b⊂β,c⊂γ,则直线a,b,c的位置关系可能是(BCD)A.两两平行B.两两垂直C.两两相交D.两两异面解析:如图①所示,在正方体ABCDA1B1C1D1中,平面ABCD、平面A1ADD1、平面A1ABB1两两垂直,则AB,AD,A1A两两相交且两两垂直,故B,C正确;CD,A1D1,BB1彼此异面,故D正确.如图②所示,设α∩β=m,β∩γ=n,α∩γ=l,在平面γ内任取一点O(O∉l,O∉n),过O作OB⊥l,OC⊥n,垂足分别为B,C.因为α⊥γ,α∩γ=l,OB⊂γ,OB⊥l,所以OB⊥α.因为m⊂α,所以OB⊥m,同理OC⊥m.因为OB∩OC=O,所以m⊥γ,同理n⊥α,l⊥β.若a,b,c两两平行,因为a⊂α,b⊂β,α∩β=m,所以a∥b∥m.又因为m⊥γ,c⊂γ,所以m⊥c,所以a⊥c,与a∥c矛盾.所以a,b,c两两平行不成立,故A错误.故选BCD.8.到空间不共面的四点距离相等的平面的个数为(C)A.1B.4C.7D.8解析:当空间四点不共面时,则四点构成一个三棱锥.①当平面一侧有一点,另一侧有三点时,如图1.令截面与四棱锥的四个面之一平行,第四个顶点到这个截面的距离与其相对的面到此截面的距离相等,这样的平面有4个;②当平面一侧有两点,另一侧有两点时,如图2,当平面过AB,BD,CD,AC的中点时,满足条件.因为三棱锥的相对棱有三对,则此时满足条件的平面有3个.所以满足条件的平面共有7个,故选C.二、填空题9.三条直线可以确定三个平面,这三条直线的公共点个数是0或1.解析:因三条直线可以确定三个平面,所以这三条直线有两种情况:一是两两相交,有1个交点;二是互相平行且不共面,没有交点....