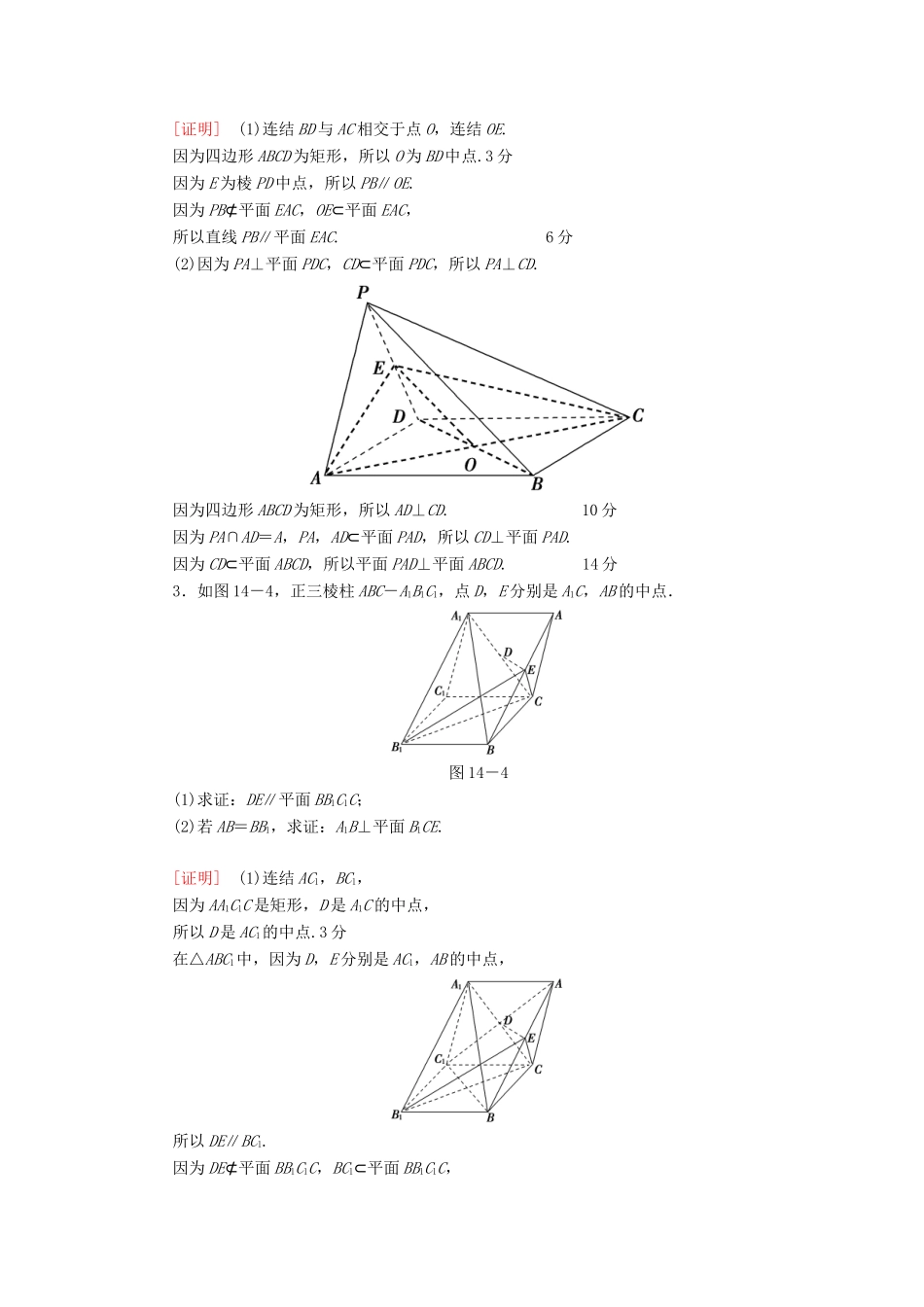
第14讲高考中的立体几何题型一|空间位置关系的证明(2016·江苏高考)如图14-1,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.图14-1求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.[解题指导](1)DE是△ABC的中位线――→DE∥AC――→DE∥A1C1DE∥平面A1C1F(2)A1C1⊥A1B1―――――→A1C1⊥平面ABB1A1―→A1C1⊥B1D――→B1D⊥平面A1C1F―→平面B1DE⊥平面A1C1F[证明](1)在直三棱柱ABC-A1B1C1中,A1C1∥AC.在△ABC中,因为D,E分别为AB,BC的中点,所以DE∥AC,于是DE∥A1C1.2分又因为DE⊄平面A1C1F,A1C1⊂平面A1C1F,所以直线DE∥平面A1C1F.4分(2)在直三棱柱ABC-A1B1C1中,A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1,所以A1A⊥A1C1.6分又因为A1C1⊥A1B1,A1A⊂平面ABB1A1,A1B1⊂平面ABB1A1,A1A∩A1B1=A1,所以A1C1⊥平面ABB1A1.8分因为B1D⊂平面ABB1A1,所以A1C1⊥B1D.10分又因为B1D⊥A1F,A1C1⊂平面A1C1F,A1F⊂平面A1C1F,A1C1∩A1F=A1,所以B1D⊥平面A1C1F.12分因为直线B1D⊂平面B1DE,所以平面B1DE⊥平面A1C1F.14分【名师点评】1.正确并熟练掌握空间中平行与垂直的判定定理与性质定理,是进行判断和证明的基础;证明面面平行、垂直时,常转化为线面的平行与垂直,再转化为线线的平行与垂直.2.证明立体几何问题,要紧密结合图形,有时要利用平面几何的相关知识,因此需要多画出一些图形辅助使用.1.(2016·苏锡常镇调研一)如图14-2,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD,M是棱AD的中点,N是棱PC的中点.图14-2(1)求证:MN∥平面PAB;(2)若平面PMC⊥平面PAD,求证:CM⊥AD.[证明](1)取PB中点E,连结EA,EN,NM,在△PBC中,EN∥BC且EN=BC,又AM=AD,AD∥BC,AD=BC,得EN∥AM,EN=AM,∴四边形ENMA是平行四边形,4分得MN∥AE,MN⊄平面PAB,AE⊂平面PAB,∴MN∥平面PAB.6分(2)过点A作PM的垂线,垂足为H. 平面PMC⊥平面PAD,平面PMC∩平面PAD=PM,AH⊥PM,AH⊂平面PAD,∴AH⊥平面PMC, CM⊂平面PMC,∴AH⊥CM.12分 PA⊥平面ABCD,CM⊂平面ABCD,∴PA⊥CM. PA∩AH=A,PA,AH⊂平面PAD,∴CM⊥平面PAD. AD⊂平面PAD,∴CM⊥AD.14分2.如图14-3,在四棱锥P-ABCD中,已知底面ABCD为矩形,PA⊥平面PDC,点E为棱PD的中点.求证:图14-3(1)PB∥平面EAC;(2)平面PAD⊥平面ABCD.[证明](1)连结BD与AC相交于点O,连结OE.因为四边形ABCD为矩形,所以O为BD中点.3分因为E为棱PD中点,所以PB∥OE.因为PB⊄平面EAC,OE⊂平面EAC,所以直线PB∥平面EAC.6分(2)因为PA⊥平面PDC,CD⊂平面PDC,所以PA⊥CD.因为四边形ABCD为矩形,所以AD⊥CD.10分因为PA∩AD=A,PA,AD⊂平面PAD,所以CD⊥平面PAD.因为CD⊂平面ABCD,所以平面PAD⊥平面ABCD.14分3.如图14-4,正三棱柱ABC-A1B1C1,点D,E分别是A1C,AB的中点.图14-4(1)求证:DE∥平面BB1C1C;(2)若AB=BB1,求证:A1B⊥平面B1CE.[证明](1)连结AC1,BC1,因为AA1C1C是矩形,D是A1C的中点,所以D是AC1的中点.3分在△ABC1中,因为D,E分别是AC1,AB的中点,所以DE∥BC1.因为DE⊄平面BB1C1C,BC1⊂平面BB1C1C,所以DE∥平面BB1C1C.6分(2)因为△ABC是正三角形,E是AB的中点.所以CE⊥AB.又因为在正三棱柱ABC-A1B1C1中,平面ABC⊥平面ABB1A1,交线为AB,所以CE⊥平面ABB1A1,从而CE⊥A1B.在矩形ABB1A1中,因为==,所以Rt△A1B1B∽Rt△B1BE,12分从而∠B1A1B=∠BB1E,因此∠B1A1B+∠A1B1E=∠BB1E+∠A1B1E=90°,所以A1B⊥B1E.又因为CE,B1E⊂平面B1CE,CE∩B1E=E,所以A1B⊥平面B1CE.14分题型二|空间几何体的体积计算如图14-5,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.图14-5(1)求证:EF⊥平面BCG;(2)求三棱锥D-BCG的体积.附:锥体的体积公式V=Sh,其中S为底面面积,h为高.【导学号:19592044】[解](1)证明:由已知得△ABC≌△DBC,因此AC=DC.2分又G为AD的中点,所以CG⊥AD.3分同理BG⊥AD,又BG∩CG=G,因此AD⊥平面BGC.5分又EF∥AD,所以EF⊥平面BCG.7分(2)在平面ABC...