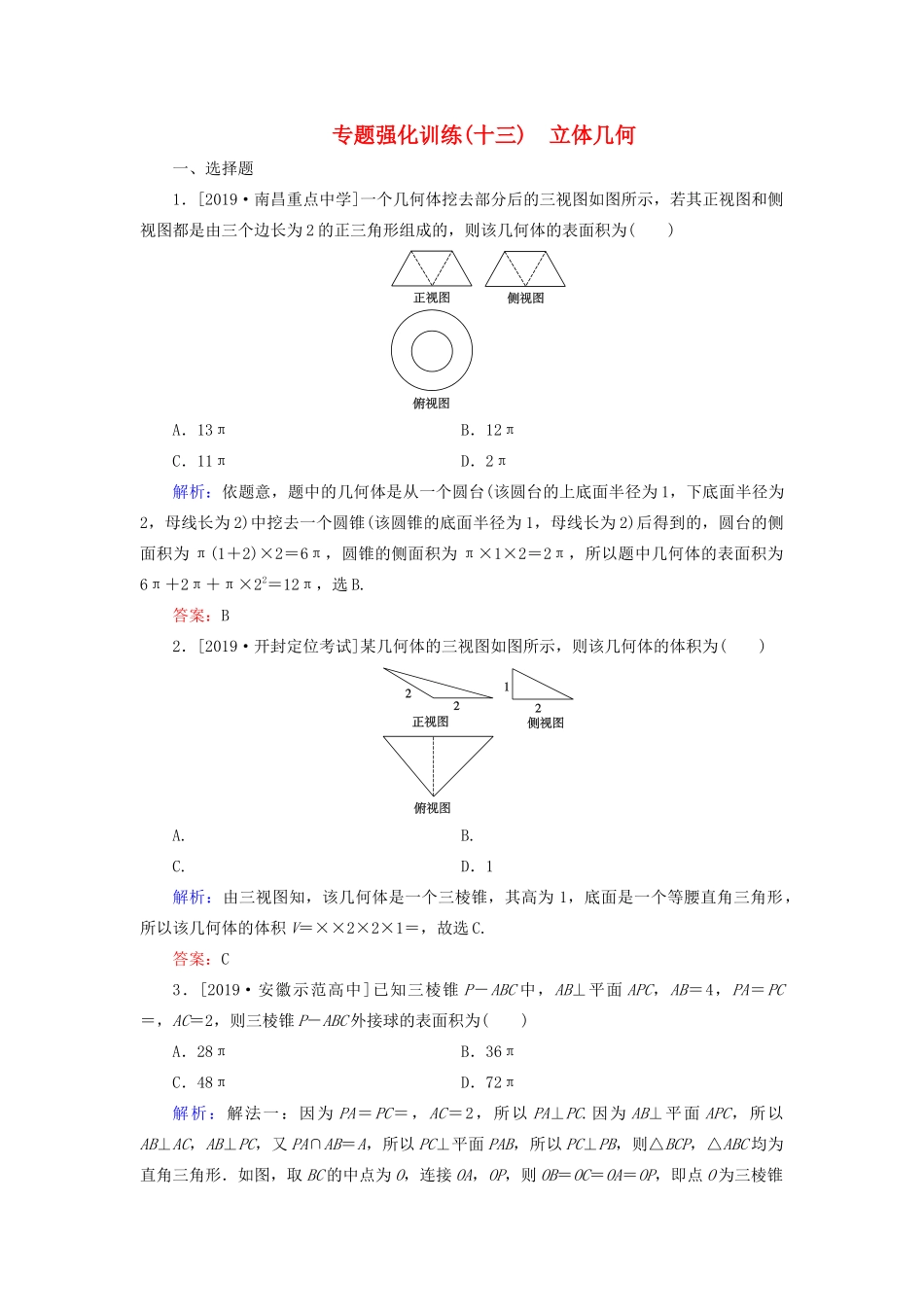
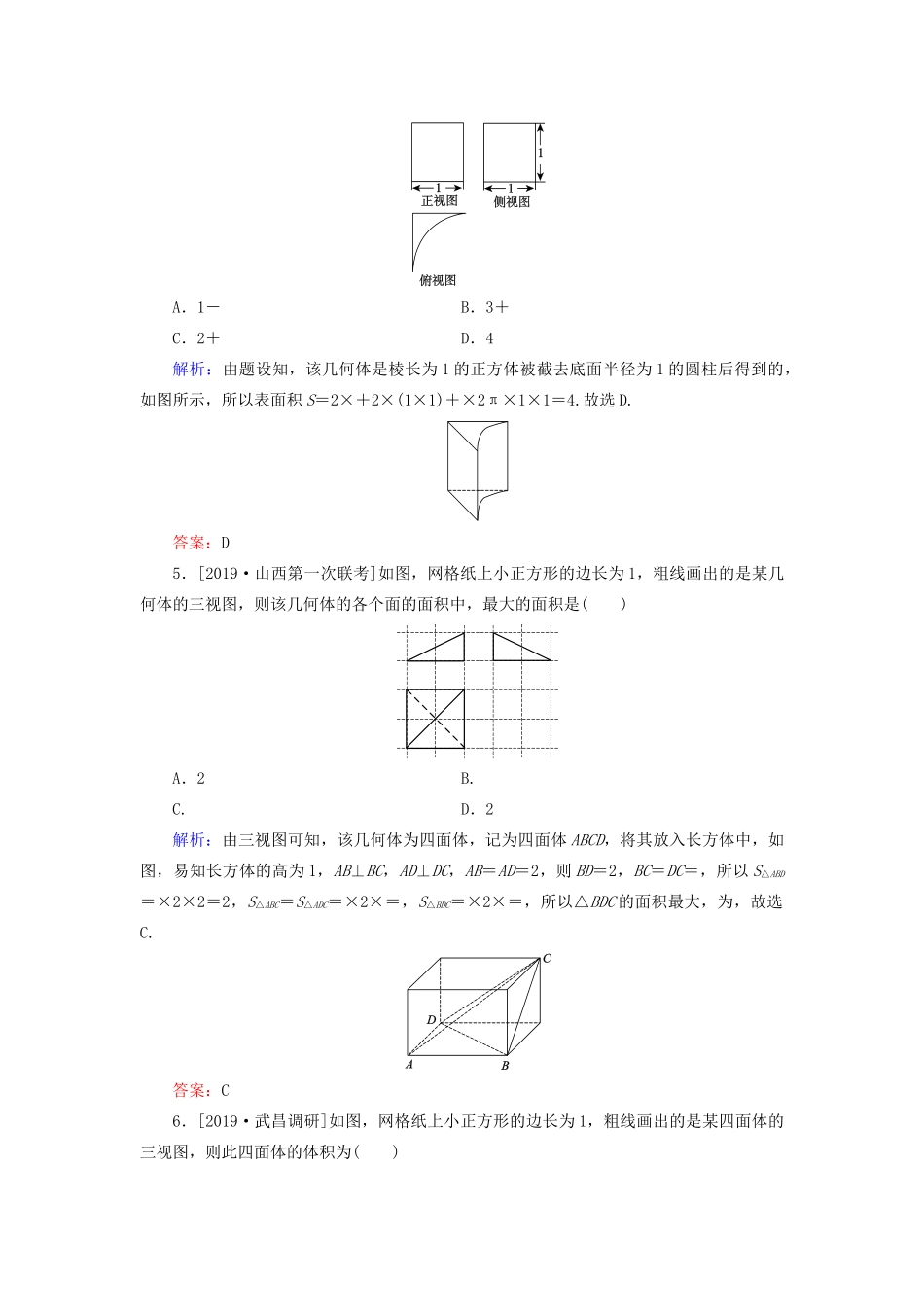
专题强化训练(十三)立体几何一、选择题1.[2019·南昌重点中学]一个几何体挖去部分后的三视图如图所示,若其正视图和侧视图都是由三个边长为2的正三角形组成的,则该几何体的表面积为()A.13πB.12πC.11πD.2π解析:依题意,题中的几何体是从一个圆台(该圆台的上底面半径为1,下底面半径为2,母线长为2)中挖去一个圆锥(该圆锥的底面半径为1,母线长为2)后得到的,圆台的侧面积为π(1+2)×2=6π,圆锥的侧面积为π×1×2=2π,所以题中几何体的表面积为6π+2π+π×22=12π,选B.答案:B2.[2019·开封定位考试]某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.1解析:由三视图知,该几何体是一个三棱锥,其高为1,底面是一个等腰直角三角形,所以该几何体的体积V=××2×2×1=,故选C.答案:C3.[2019·安徽示范高中]已知三棱锥P-ABC中,AB⊥平面APC,AB=4,PA=PC=,AC=2,则三棱锥P-ABC外接球的表面积为()A.28πB.36πC.48πD.72π解析:解法一:因为PA=PC=,AC=2,所以PA⊥PC.因为AB⊥平面APC,所以AB⊥AC,AB⊥PC,又PA∩AB=A,所以PC⊥平面PAB,所以PC⊥PB,则△BCP,△ABC均为直角三角形.如图,取BC的中点为O,连接OA,OP,则OB=OC=OA=OP,即点O为三棱锥P-ABC外接球的球心.在Rt△ABC中,AC=2,AB=4,则BC=6,所以外接球的半径R=3,所以三棱锥P-ABC外接球的表面积S=4πR2=36π,故选B.解法二:因为PA=PC=,AC=2,所以PA⊥PC,△ACP为直角三角形.如图,取AC的中点为M,则M为△PAC外接圆的圆心.过M作直线n垂直于平面PAC,则直线n上任意一点到点P,A,C的距离都相等.因为AB⊥平面PAC,所以AB平行于直线n.设直线n与BC的交点为O,则O为线段BC的中点,所以点O到点B,C的距离相等,则点O即三棱锥P-ABC外接球的球心.因为AB⊥平面PAC,所以AB⊥AC,又AC=2,AB=4,所以BC=6,则外接球的半径R=3,所以三棱锥P-ABC外接球的表面积S=4πR2=36π,故选B.解法三:因为PA=PC=,AC=2,所以PA⊥PC,又AB⊥平面PAC,所以可把三棱锥P-ABC放在如图所示的长方体中,此长方体的长、宽、高分别为,,4,则三棱锥P-ABC的外接球即长方体的外接球,长方体的体对角线即长方体外接球的直径,易得长方体的体对角线的长为6,则外接球的半径R=3,所以三棱锥P-ABC外接球的表面积S=4πR2=36π,故选B.答案:B4.[2019·唐山摸底]已知某几何体的三视图如图所示(俯视图中曲线为四分之一圆弧),则该几何体的表面积为()A.1-B.3+C.2+D.4解析:由题设知,该几何体是棱长为1的正方体被截去底面半径为1的圆柱后得到的,如图所示,所以表面积S=2×+2×(1×1)+×2π×1×1=4.故选D.答案:D5.[2019·山西第一次联考]如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最大的面积是()A.2B.C.D.2解析:由三视图可知,该几何体为四面体,记为四面体ABCD,将其放入长方体中,如图,易知长方体的高为1,AB⊥BC,AD⊥DC,AB=AD=2,则BD=2,BC=DC=,所以S△ABD=×2×2=2,S△ABC=S△ADC=×2×=,S△BDC=×2×=,所以△BDC的面积最大,为,故选C.答案:C6.[2019·武昌调研]如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则此四面体的体积为()A.B.16C.32D.48解析:由三视图知,该四面体可以看作是正方体中的三棱锥P-ABC,如图,由已知可得AB=4,AC=4,△ABC是直角三角形,所以S△ABC=AB×AC=×4×4=8,所以四面体PABC的体积V=×8×4=,故选A.答案:A7.[2019·洛阳联考]四棱锥S-ABCD的所有顶点都在同一个球面上,底面ABCD是正方形且和球心O在同一平面内,当此四棱锥的体积取得最大值时,其表面积等于8+8,则球O的体积等于()A.B.C.16πD.解析:由题意得,当此四棱锥的体积取得最大值时,四棱锥为正四棱锥.如图,连接AC,则球心O为AC的中点,连接SO,设球O的半径为R,则AC=2R,SO=R,∴AB=BC=R.取AB的中点为E,连接OE,SE,则OE=BC=R,SE==R. 该四棱锥的体积取得最大值时,其表面积等于8+8,∴(R)2+4××R×R=8+8,解得R=2,∴球O的...