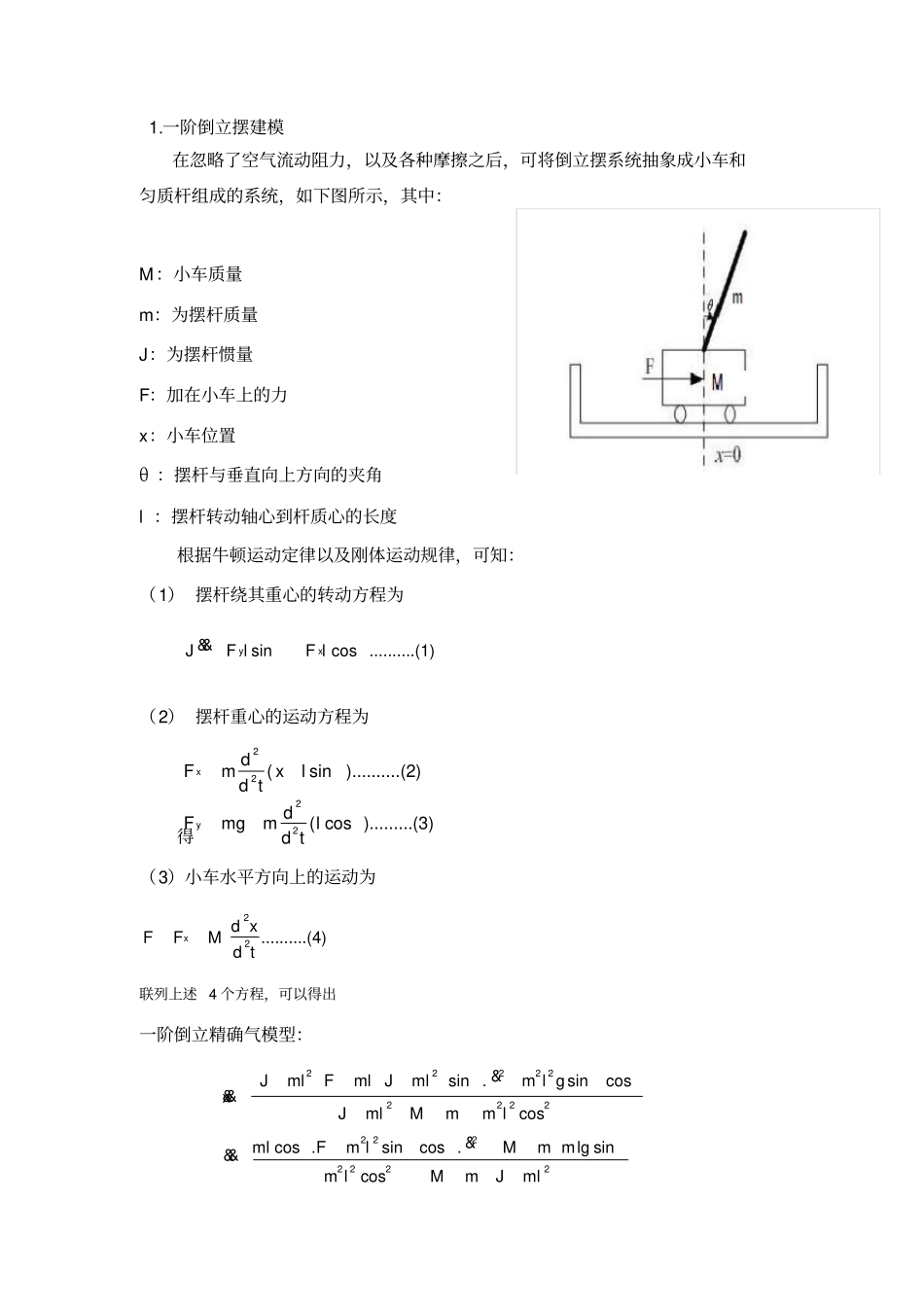
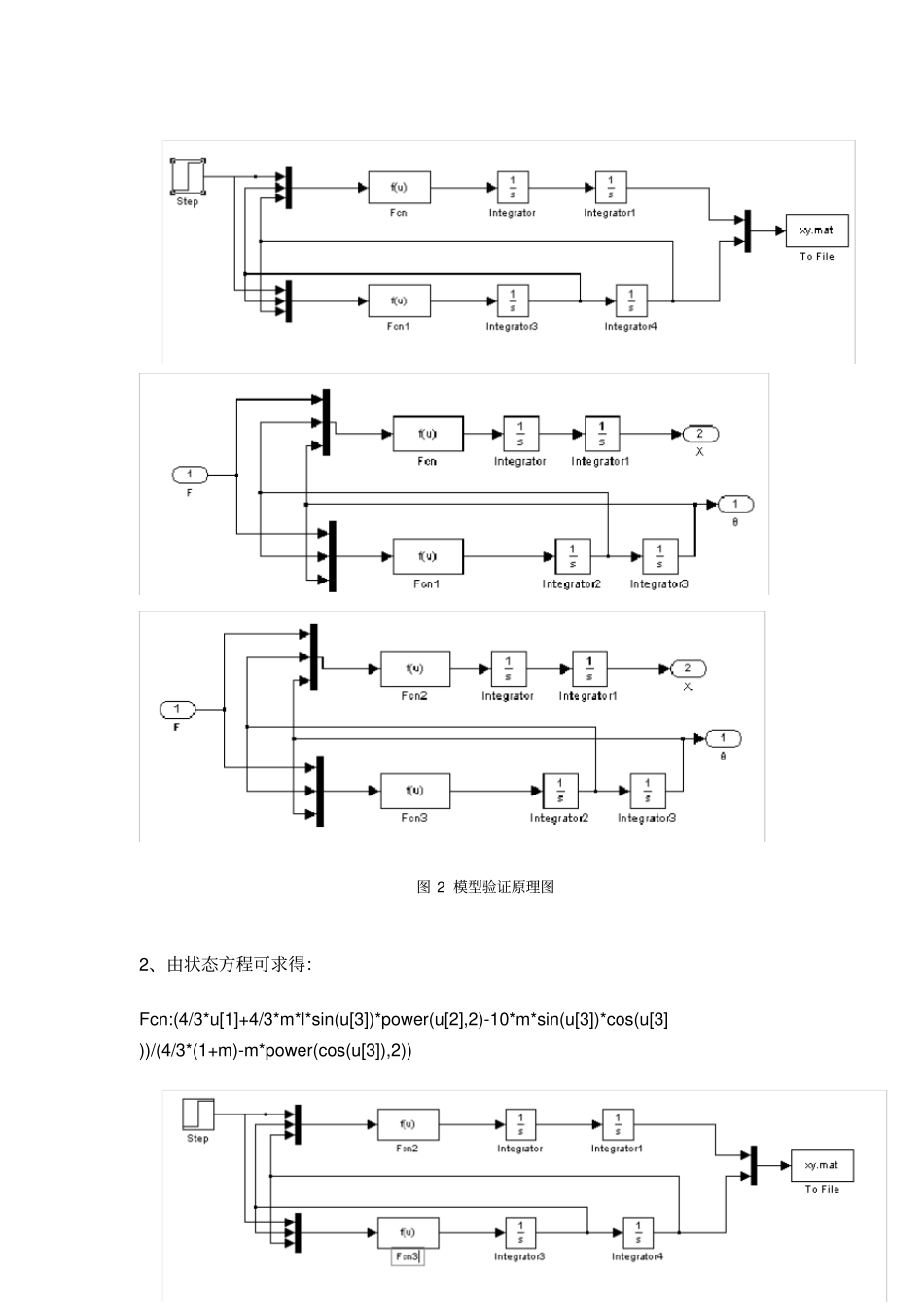
1.一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示,其中:M:小车质量m:为摆杆质量J:为摆杆惯量F:加在小车上的力x:小车位置θ:摆杆与垂直向上方向的夹角l:摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律,可知:(1)摆杆绕其重心的转动方程为(2)摆杆重心的运动方程为得(3)小车水平方向上的运动为22..........(4)xdxFFMdt联列上述4个方程,可以得出一阶倒立精确气模型:2222222222222222sin.sincoscoscos.sincos.lgsincosJmlFmlJmlmlgxJmlMmmlmlFmlMmmmlMmJml&&&&&&sincos..........(1)yxJFlFl&&2222(sin)..........(2)(cos).........(3)xydFmxldtdFmgmldt式中J为摆杆的转动惯量:32mlJ若只考虑θ在其工作点附近θ0=0附近(1010)的细微变化,则可以近似认为:1cossin022..2222..)(lg)()()(MmlmMJmlFmmMMmlmMJglmFmlJx2.2模型建立及封装1、建立以下模型:图2模型验证原理图2、由状态方程可求得:Fcn:(4/3*u[1]+4/3*m*l*sin(u[3])*power(u[2],2)-10*m*sin(u[3])*cos(u[3]))/(4/3*(1+m)-m*power(cos(u[3]),2))Fcn1:(cos(u[3])*u[1]+m*l*sin(u[3])*cos(u[3])*power(u[2],2)-10*(1+m)*sin(u[3]))/(m*l*power(cos(u[3]),2)-4/3*l*(1+m))Fun2:(4*u[1]-30*m*u[3])/(4+m)Fun3:(u[1]-10*(1+m)*u[3])/(m*l-4/3*l*(1+m))(其中J=mL^2/3,小车质量M=1kg,倒摆振子质量m=1Kg,倒摆长度l=1m,重力加速度g=10m/s^2)将以上表达式导入函数。3、匡选要封装区后选择[Edit>>CreateSubsystem]便得以下系统:图3子系统建立4、鼠标右击子系统模块,在模块窗口选项中选择[Edit>>EditMask>>Parameters],则弹出如下窗口,添加参数m和l。图4添加参数5、将精确模型subsystem和简化模型subsystem1组合成以下系统以供验证(输入信号是由阶跃信号合成的脉冲,幅值及持续时间为0.1s)。图5系统模块封装3仿真验证3.1实验设计假定使倒立摆在(θ=0,x=0)初始状态下突加微小冲击力作用,则依据经验知,小车将向前移动,摆杆将倒下。3.2编制绘图子程序1、新建M文件输入以下程序并保存。clcloadxy.matt=signals(1,:);%读取时间信号f=signals(2,:);%读取作用力F信号x=signals(3,:);%读取精确模型中的小车位置信号q=signals(4,:);%读取精确模型中倒摆摆角信号xx=signals(5,:);%读取简化模型中的小车位置信号qq=signals(6,:);%读取简化模型中倒立摆摆角信号figure(1)%定义第一个图形hf=line(t,f(:));%连接时间-作用力曲线gridon;xlabel('Time(s)')%定义横坐标ylabel('Force(N)')%定义纵坐标axis([0100.12])%定义坐标范围axet=axes('Position',get(gca,'Position'),...'XAxisLocation','bottom',...'YAxisLocation','right','color','none',...'XColor','k','YColor','k');%定义曲线属性ht=line(t,x,'color','r','parent',axet);%连接时间-小车位置曲线ht=line(t,xx,'color','r','parent',axet);%连接时间-小车速度曲线ylabel('Evolutionofthexposition(m)')%定义坐标名称axis([0100.1])%定义坐标范围title('Responsexandx''inmetertoaf(t)pulseof0.1N')%定义曲线标题名称gtext('\leftarrowf(t)'),gtext('x(t)\rightarrow'),gtext('\leftarrowx''(t)')figure(2)hf=line(t,f(:));gridonxlabel('Time')ylabel('Force(N)')axis([0100.12])axet=axes('Position',get(gca,'Position'),...'XAxisLocation','bottom',...'YAxisLocation','right','color','none',...'XColor','k','YColor','k');ht=line(t,q,'color','r','parent',axet);ht=line(t,qq,'color','r','parent',axet);ylabel('Angleevolution(rad)')axis([01-0.30])title('Response\theta(t)and\theta''inradtoaf(t)pulseof0.1N')gtext('\leftarrowf(t)'),gtext('\theta(t)\rightarrow'),gtext('\leftarrow\theta''(t)'3.3仿真验证2、在系统模型中,双击子系统模块,则会弹出一个新窗口,在新窗口中输入m和l值,点击OK并运行,如图7所示。图6参数输入3、运行M文件程序,执行该程序的结果如图8所示。图7模型验证仿真结果从中可见,在0.1N的冲击力下,摆杆倒下(θ由零逐步增大...