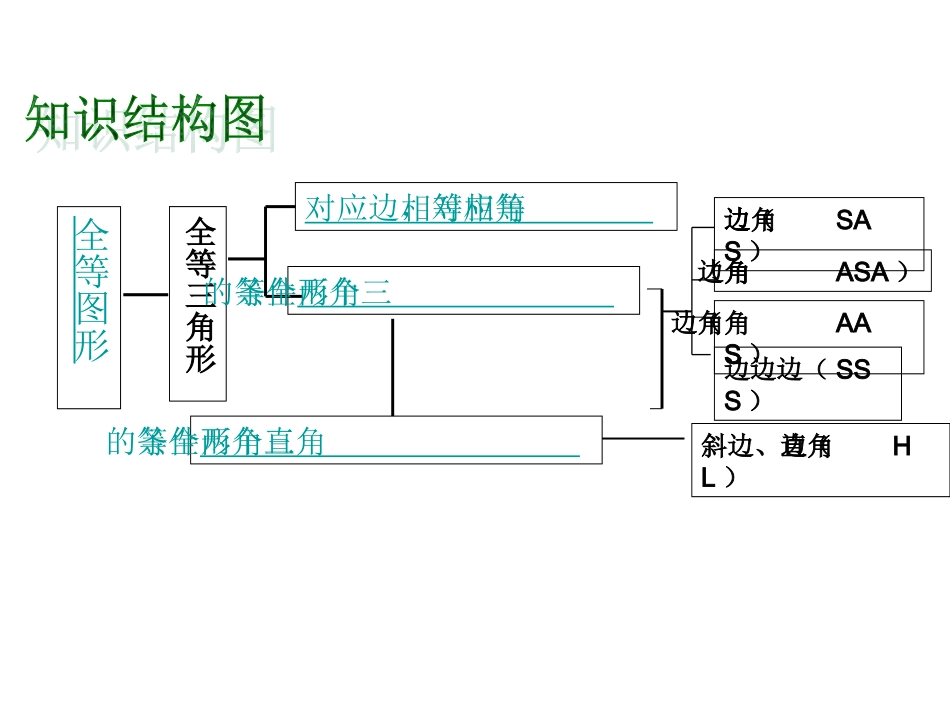
全等图形全等三角形对应边相等,对应角相等两个三角形全等的条件两个直角三角形全等的条件边角边(SAS)角边角(ASA)角角边(AAS)边边边(SSS)斜边、直角边(HL)能够完全重合的图形叫全等图形。下列各组中是全等图形的是()A.两个周长相等的等腰三角形B.两个面积相等的长方形C.两个面积相等的直角三角形D.两个周长相等的圆全等图形的形状和大小都相同.1.如图,△ABC≌△ADE,则,AB=,∠E=∠.若∠BAE=120°,∠BAD=40°,则∠BAC=.2.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是()A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBDD.AD∥BC,且AD=BCDACB3.如图,已知AB=DC,AD=BC,E,F在DB上两点,且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=()A.150°B.40°C.80°D.90°ADBCEF1.如图,AB=AC,要使△ABE≌△ACD,应添加的条件是(添加一个条件即可).2.根据下列已知条件,能唯一画出△ABC的是()A.AB=3,BC=4,CA=8B.AB=4,BC=3,∠A=30°C.∠A=60°,∠B=45°,AB=4D.∠C=90°,AB=64.用五根木棒钉成如下四个图形,具有稳定性的有()A.1个B.2个C.3个D4个5.在正方形网格内,小格的顶点叫做格点.以点D、E为两个顶点,作出所有位置不同的格点三角形,使所作的格点三角形与△ABC全等.这样的格点三角形最多可以画出()6.如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是()A.PM>PNB.PM<PNC.PM=PND.不能确定5.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=cm.6.如图,△ABC中,ADBC⊥于D,若BD=AD,FD=CD.求证(1)∠FBD=CAD∠;(2)BEAC.⊥7.如图,已知AB=DC,DB=AC求证:∠ABD=DCA∠8.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,求证:(1)△BCEACD≌△;(2)CF=CH;(3)△FCH是等边三角形;(4)FHBD∥.变式:如图,在线段AE同侧作两个等边三角形△ABC和△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点,则△CPM是()A.钝角三角形B.直角三角形C.等边三角形D.非等腰三角形1.如图,MN∥PQ,AB⊥PQ,点A、D、B、C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=.2.已知:如图,DE⊥AB,DF⊥AC,垂足分别为E,F,BD=CD,BE=CF.(1)求证:AD平分∠BAC;(2)写出AC、AE、BE之间的数量关系.课堂小结:本节课你有哪些收获?