第二讲立体几何VIP免费

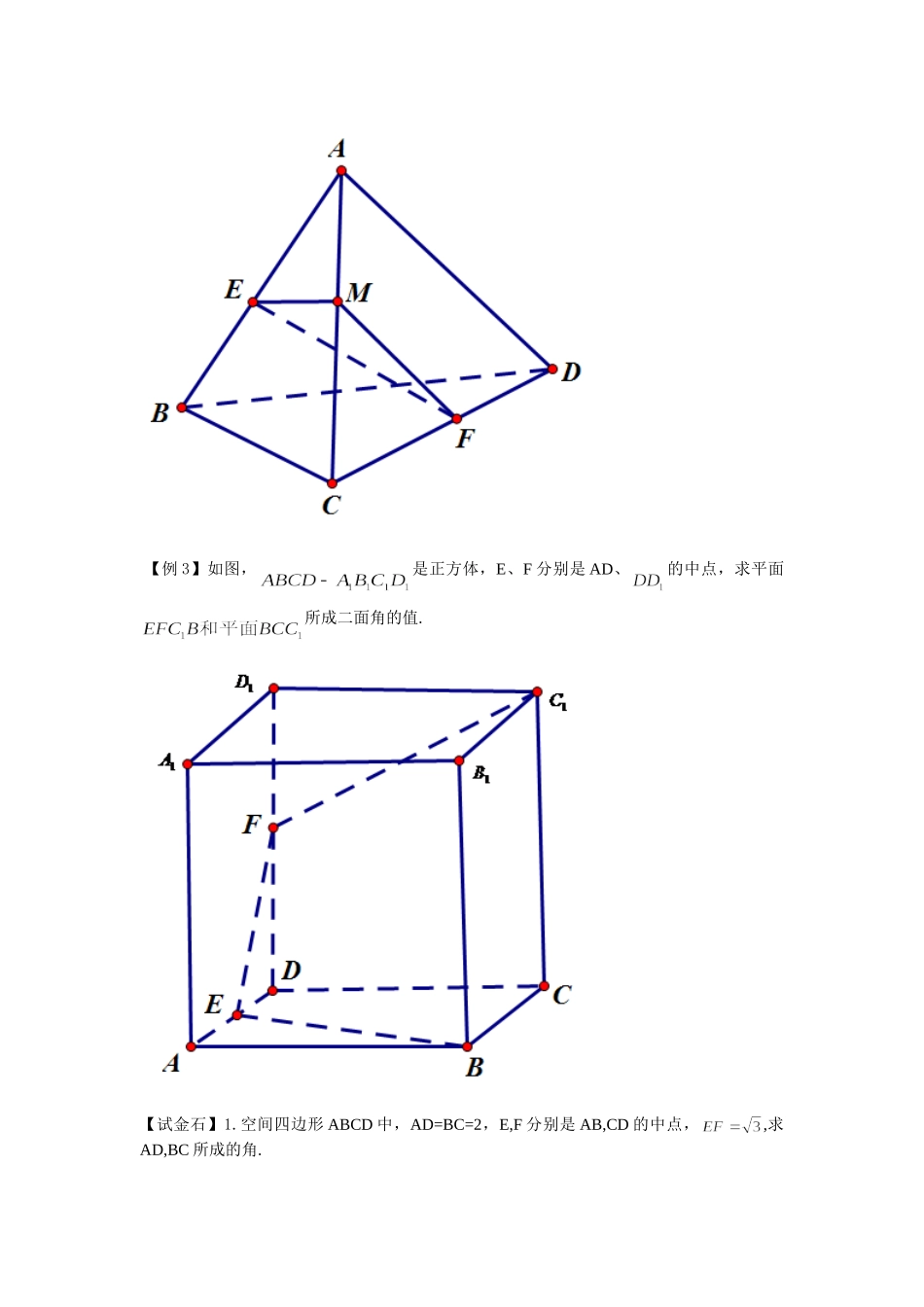
专题一复数与立体几何(第2讲)【预习】阅读课本132-135页，并完成导学【预习目标】回顾空间图形和线面关系．【导引】线、面关系(以下l,l1,l2,...表示直线，,...表示平面)直线之间关系关系种类平行：l、l1在同一平面上，且ll1=；相交：ll1；异面：ll1=且l、l1不共面；(l、l1共面l∥l1或ll1．)平行关系判定l1∥l，l2∥ll1∥l2；l1，l2l1∥l2；l1∥，l1，l2=l1∥l2；∥，l1=,，l2=l∥l2．垂直关系判定l2∥l,，l1ll1l2；l1,，l2l1l2；l为l1在平面上的正射影，l2l1l2l．(三垂线定理)异面直线夹角l1，l2为异面直线，过l1上点A作l∥l2，l1^l2=l1^l．直线与平面关系关系种类l；l∥：l=；l：对任意l1，ll1；l与斜交：l且l不垂直于．垂直关系判定l1，l2，l1l2，ll1且ll2l；,，，l=l；,，l1=;，l且ll1l．平行关系判定l1,，l∥l1l∥；l1，ll1l∥；∥,，l=l∥．直线平面夹角l与斜交，l1为l在上的正射影，则l与的夹角=l^l1．平面之间关系关系种类||：=；：与的二面角为90；一般相交：且，不垂直．平面平行判定l1，l2，l1l2，l1∥且l2∥∥；l1，l2，l1l2，，，l1∥，l2∥∥；l，l∥．平面垂直判定l，l；平面交角二面角：交于棱l的两个半平面,构成的图形，记作-l-；二面角的平面角：过棱l上一点、分居于,上且垂直于l的两条半直线形成的角，平面角的大小(在0180)即为两面角的大小；平面交角：相交平面所形成的四个二面角中，不超过90的那个平面角．【试试看】1.若长方体三个面的面积分别是则长方体的体积是__________.2.一圆锥的母线长为50cm，高为40cm，则该圆锥的侧面积为__________3.已知两条不同的直线两个不同的平面给出下列命题：①若垂直于内的两条相交直线，则；②若则平行于内的所有直线；③若；④；⑤.其中正确命题的序号是__________.4.球的大圆面积扩大到原来的8倍，那么球的表面积扩大为原来的__________倍.【本课目标】1.回顾立体几何的基本知识点，能进行相关的计算和证明.2.培养学生分析问题、解决问题的能力，提高学生的读图能力．【重点】线面关系的证明与计算．【难点】空间图形的理解.【导学】任务1：柱锥球的表面积及体积的计算．【例1】一个圆柱的底面积是正方形，那么该圆柱的侧面积为（）A.B.C.D.【试金石】（1）圆锥的母线长为1，侧面展开图的圆心角为，该圆锥的体积是（）A.B.C.D.任务2：了解线、面关系的证明与计算．【例2】点A是所在平面外一点，AD=BC，E、F分别是AB、CD的中点，且，求异面直线AD和BC所成的角.【例3】如图，是正方体，E、F分别是AD、的中点，求平面所成二面角的值.【试金石】1.空间四边形ABCD中，AD=BC=2，E,F分别是AB,CD的中点，,求AD,BC所成的角.2.如图，已知圆锥的高SO与母线的夹角为，AB为底面圆的直径，C为圆周上一点，AC=4且AC所对圆心角.求（1）圆锥侧面积和体积；（2）SA与底面所成角；（3）二面角S-AC-O的大小.【检测】1.在正方体中与成角的面对角线的条数是（）A．4条B．6条C．8条D．10条2.若母线长为4的圆锥的轴截面的面积为8，则圆锥的侧面积为．3.将边长为1的正方形ABCD，沿对角线AC折起，使BD=.求三棱锥D-ABC的体积.【导练】一.选择题1．设a,b是两条不同的直线，是两个不同的平面，则下列四个命题①②③④其中正确的命题的个数是（）A．0个B．1个C．2个D．3个2.已知正三棱柱的侧棱长与底面边长相等，则与侧面所成角的正弦值等于（）A．B．C．D．二.填空题3．在正三棱柱中，AB=1，侧棱长为，则与侧面所成角是．4．在四面体ABCD中，E、F分别是AC与BD的中点，若CD=2AB=4，,则EF与CD所成的角为．三.解答题5．如图，在三棱锥S-ABC中，为正三角形，S在平面ABC内的射影O在的平分线CD上.(1)求证；（2）若BC=2，SC=1,且，求二面角A-SC-B的余弦值.