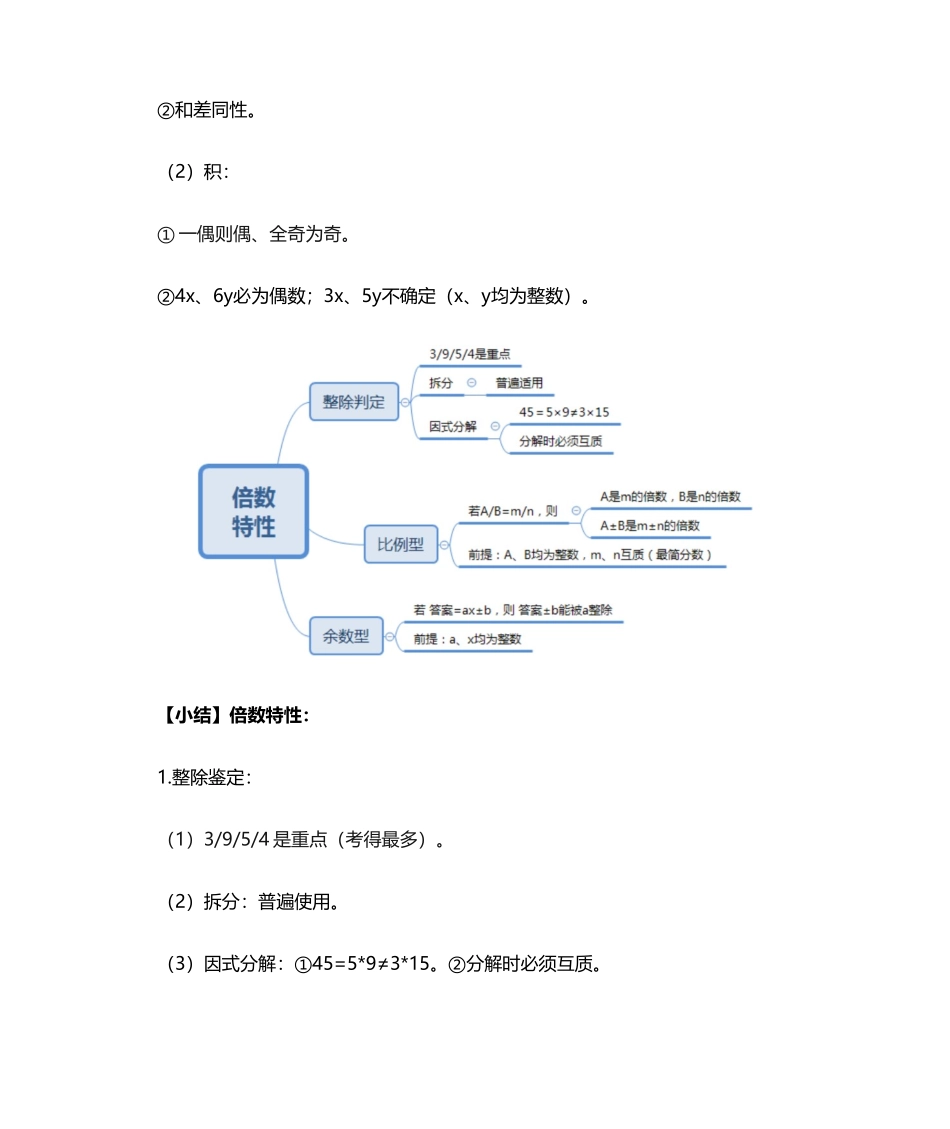
数量关系1.三大措施(必考题型的措施):代入排除、数字特性、方程法。2.六大题型:工程问题、行程问题;经济利润、排列组合;容斥原理、最值问题。【小结】代入排除:1.范围:(1)特定题型:年龄、不定方程、余数、多位数。(2)选项信息充足:选项为一组数(例1);可转化为一组数(例2)。(3)题目复杂:题目长、主体多,关系乱(例3)。2.措施:(1)先排除:大小、奇偶、倍数、尾数(出现5和10的倍数)。(2)再代入:简朴入手、最值思想。【小结】奇偶特性:1.范围:(1)不定方程:一般优先考虑奇偶性。(2)平均提成两份、2倍(4、6、8等偶数倍):必然是偶数。(3)知和求差、知差求和。(4)质数:逢质必2。2.措施:(1)和差:①同奇同偶则为偶、一奇一偶则为奇。②和差同性。(2)积:①一偶则偶、全奇为奇。②4x、6y必为偶数;3x、5y不确定(x、y均为整数)。【小结】倍数特性:1.整除鉴定:(1)3/9/5/4是重点(考得最多)。(2)拆分:普遍使用。(3)因式分解:①45=5*9≠3*15。②分解时必须互质。2.比例型:出现分数、比例、百分数、倍数时使用。(1)若A/B=m/n,则:①A是m的倍数,B是n的倍数。②A±B是m±n的倍数。(2)前提:A、B均为整数,m、n互质(最简分数)。3.余数型:(1)若答案=ax±b,则答案∓b能被a整除。(2)前提:a、x均为整数。【小结】方程法:1.一般方程:设、列、解三步走。(1)设未知数:①设小不设大(防止分数);②最大信息化(以便列式);③求谁设谁(防止陷阱)。(2)列方程:“共、是、比、相等”等明显的等量关系。(3)解方程:①约分:如3600=400x+800y,先消掉2个0;②消元:求谁留谁。2.不定方程:(1)主流:未知数必须为整数:①奇偶特性:系数一奇一偶。②倍数特性:系数与常数有公因子。例如5a+3b=25,5a、15均有公因子5。③尾数特性:系数尾数为5或0。④代入排除:运用题干条件验证。(2)非主流:①未知数未必为整数;②求算式而非单一未知数。(3)赋0法:设某个未知数为零,再求出其他未知数。【小结】工程问题:1.赋值总量型:(1)识别:题干只给了多种竣工时间。(2)措施:赋值总量——算出效率——列式求解。(3)技巧:总量一般设公倍。2.赋值效率型:(1)识别:题干给出了效率比、效率倍数等。(2)措施:赋值效率——求出总量——列式求解。(3)技巧:按照比例设效率,设值尽量设整数。3.给详细值型:(1)识别:题干有效率、总量的详细值。(2)措施:代公式——列方程求解。【小结】行程问题:1.一般行程:火车过桥:车长+桥长。(1)旅程=速度*时间。(2)平均速度:①总距离/总时间。②等距离上下坡、来回:V=2ab/(a+b)。2.相对行程:(1)相遇追及:①相遇:S和=V和*T遇。②追及:S差=V差*T追。(2)多次运动:①线形第n次相遇:(2n-1)S=V和*T。②环形第n次相遇:n圈=V和*T。③环形第n次追及:n圈=V差*T。(3)顺水逆水:①顺水:S=(V船+V水)*T顺。②逆水:S=(V船-V水)*T逆。3.比例行程:(1)S一定,V与T成反比。(2)V(T)一定,S与T(V)成正比。【小结】经济利润:1.基础经济:(1)求详细钱数:方程法。(2)无详细钱数求比例:赋值(常赋成本为100)。(3)常用公式:①利润=售价-成本。②利润率=利润/成本。③折扣(9折、85折)。2.分段计算:(1)常见类型:水电费、出租车费、税费等等。(2)措施:按原则分开计算,最终加和。3.合并付费:(1)题型:将分开购置的物品一起购置需要多少钱。(2)措施:①找到原价超过最大优惠力度的钱数。②计算较小金额的原价,按最大优惠计算。【小结】排列组合:1.排列组合:(1)概念:①分类用加法(要么……要么……)。只发生一种状况。②分步用乘法(先……再……)。同步发生。③有序用排列(不可互换,用A)。④无序用组合(可以互换,用C)。⑤判断有序或无序:将选出的次序挑两个互换,影响成果用A,不影响成果用C。(2)题型:①要相邻:捆绑法,先捆再排。②不相邻:插空法,先排再插。③凑数字:枚举法,按序枚举。从大到小,不重不漏。2.概率:(1)概率=满足规定的状况数/所有的状况数。用分子或分母的倍数特性,迅速排除或选...