高一数学对数函数的图象和性质二VIP免费

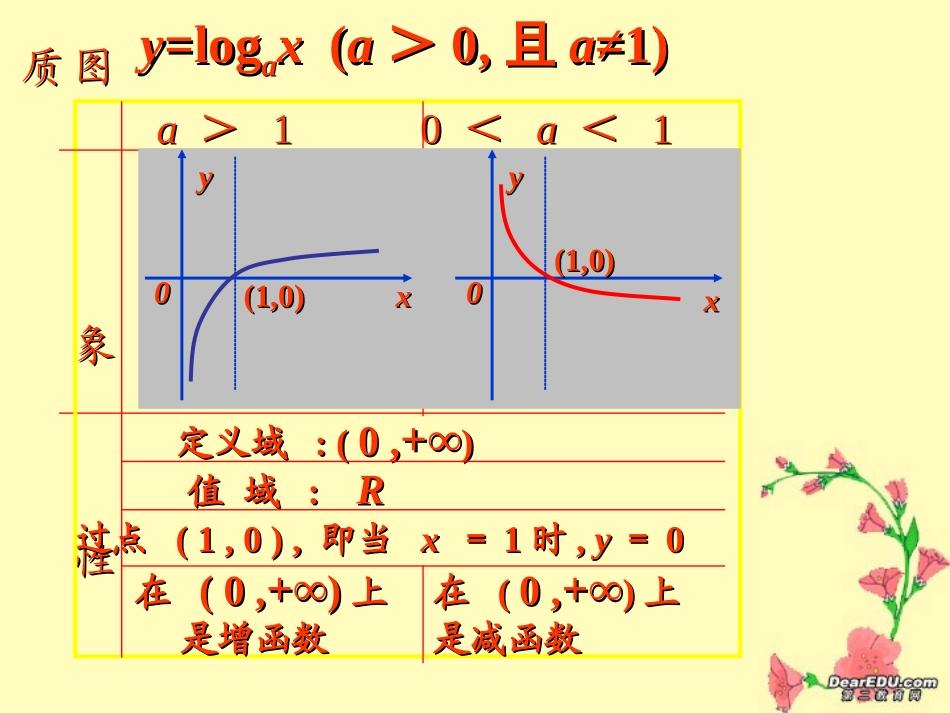
一、复习准备：提问：对数函数的图象和性质？aa＞＞1010＜＜aa＜＜11yy=log=logaaxx((aa＞＞0,0,且且aa≠1)≠1)图象性图象性质质定义域定义域:(:(0,0,+∞+∞))值域值域::RR过点过点(1,0),(1,0),即当即当xx＝＝11时时,,yy＝＝00在在(0,(0,+∞+∞))上上是增函数是增函数在在((0,0,+∞+∞))上上是减函数是减函数yyxx00yyxx00(1,0)(1,0)(1,0)(1,0)二、基础练习：1.根据对数函数的图象和性质填空．①已知函数，则当时，；当时，；xy2log0xy1xy当时，；当时，．10xy4xy②已知函数，则当时，；当时，；xy31log10xy1xy当时，；当时，；当时，．5xy20xy2yx（小结：数形结合法求值域、解不等式）2.判断下列函数的奇偶性：)1ln()(2xxxf.)112lg(.3的奇偶性判断函数练习xy奇函数3.（1）证明函数在上是增函数。)1(log)(22xxf),0(（2）探究：函数在上是减函数还是增函数？)1(log)(22xxf)0,(4.求函数的单调区间．0.2()log(45)fxx解法：先求定义域→设，讨论u的单调性→讨论单调性→结论545()4uxx()u（小结：复合函数单调性的求法及规律：“同增异减”→变底训练）三、巩固练习1.比较大小：loglog(0aaea和且a1)2221loglog(1)()2aaaR和；2．已知恒为正数，求的取值范围．log(31)aaa3．求函数的定义域及值域．(注意：函数值域的求法)2()lg(8)fxx4．函数在[2，4]上的最大值比最小值大1，求a的值；xyalog5.求函数的最小值．23log(610)yxx（注意：利用函数单调性求函数最值的方法，复合函数最值的求法．）.]4,2[,5log2)(log)(.425.0225.0的最值求函数例xxxxf有则解：令]21,1[,log25.0txt4)1(5222ttty;8)(,41maxxfxt时即当416)(221minxfxt时，即当