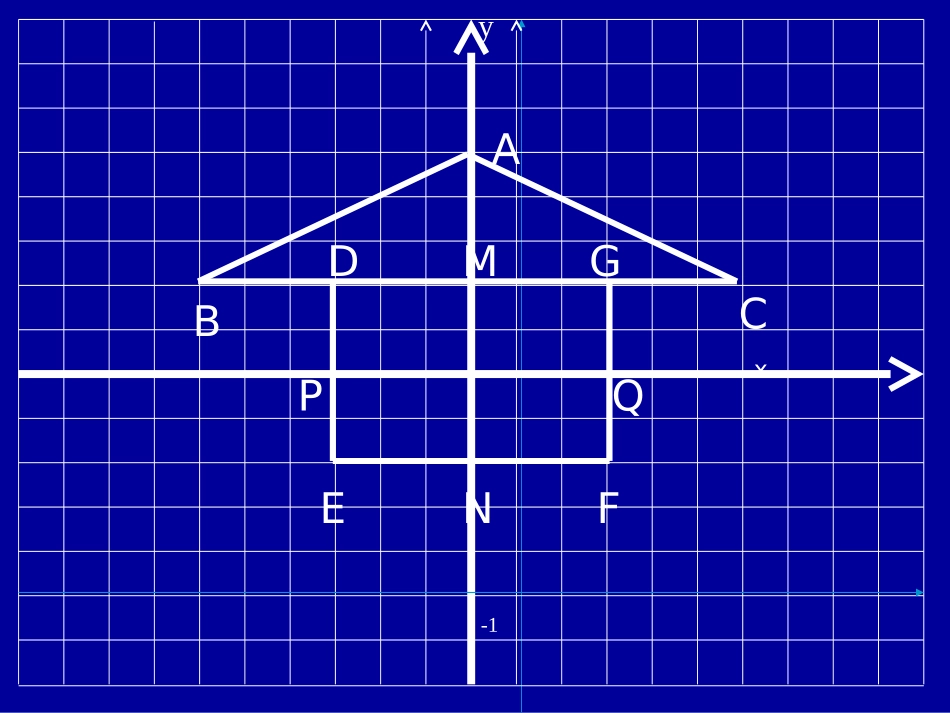
3.23.2平面直角坐标系(二)平面直角坐标系(二)例例22请在坐标纸上建立平面直角坐标系,然后描出请在坐标纸上建立平面直角坐标系,然后描出下列各点下列各点AA((00,,55),),BB((-6-6,,22),),CC((66,,22),),DD((-3-3,,22),),EE((-3-3,,-2-2),),FF((33,,--22),),GG((33,,22))-1yxABCDGEFMNPQ1.1.观察点观察点AA,,MM,,NN的坐标,点的坐标,点PP,,QQ的坐标。那的坐标。那么坐标轴上的点有什么特征?么坐标轴上的点有什么特征?2.2.各点分别到各点分别到xx轴、轴、yy轴的距离是多少?轴的距离是多少?3.3.观察点观察点B,CB,C和和D,GD,G和和E,FE,F。它们的横、纵坐标。它们的横、纵坐标有什么特征?线段有什么特征?线段BCBC和和EFEF与与xx轴位置上有什么关轴位置上有什么关系?系?4.4.观察点观察点D,ED,E和和F,GF,G。它们的横、纵坐标有什么。它们的横、纵坐标有什么特征?线段特征?线段DEDE和和FGFG与与yy轴位置上有什么关系?轴位置上有什么关系?基本题:基本题:1.1.在在yy轴上的点的横坐标是(),在轴上的点的横坐标是(),在xx轴上轴上的点的纵坐标是()的点的纵坐标是()..2.2.点点AA((22,,-3-3)关于)关于xx轴对称的点轴对称的点的坐标是()的坐标是()..3.3.点点BB((-2-2,,11)关于)关于yy轴对称的点轴对称的点的坐标是()的坐标是()..4.点M(-8,12)到x轴的距离是(),到y轴的距离是().5.点(4,3)与点(4,-3)的关系是().(A)关于原点对称(B)关于x轴对称(C)关于y轴对称(D)不能构成对称关系6.6.若点若点PP((2m-12m-1,,33)在第二象限,则()在第二象限,则())..((AA))m>1/2m>1/2((BB))m<1/2m<1/2((CC))m≥-1/2m≥-1/2((DD))m≤1/2m≤1/27.7.如果同一直角坐标系下两个点的横坐标相同,如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线()那么过这两点的直线()..((AA)平行于)平行于xx轴(轴(BB)平行于)平行于yy轴轴((CC)经过原点()经过原点(DD)以上都不对)以上都不对提高题提高题::1.1.若若mn=0mn=0,则点,则点PP((mm,,nn)必定在)必定在上上..2.2.已知点已知点PP((aa,,bb),),QQ((33,,66),且),且PQ∥xPQ∥x轴,则轴,则bb的值为的值为()()..3.3.点(点(mm,,-1-1)和点()和点(22,,nn)关于)关于xx轴对轴对称,则称,则mnmn等于等于()()..((AA))-2-2((BB))22((CC))11((DD))-1-14.4.实数实数xx,,yy满足满足xx22+y+y22=0=0,则点,则点PP((xx,,yy)在)在()()..((AA)原点()原点(BB))xx轴正半轴轴正半轴((CC)第一象限()第一象限(DD)任意位置)任意位置5.5.点点AA在第一象限,当在第一象限,当mm为何值为何值()()时,时,点点AA((m+1m+1,,3m-53m-5)到)到xx轴的距离是它到轴的距离是它到yy轴轴距离的一半距离的一半..思考题:思考题:已知边长为已知边长为22的正方形的正方形OABCOABC在直在直角坐标系中(如图),角坐标系中(如图),OAOA与与yy轴的夹角为轴的夹角为30°30°,那么点,那么点AA的坐的坐标为标为,点,点CC的坐标为的坐标为,点,点BB的坐标为的坐标为。。小结:小结:通过今天这节课的内容,你学到了什么?通过今天这节课的内容,你学到了什么?作业:作业:1.1.必做题:习题必做题:习题3.33.3第第11、、33题题2.2.选做题:习题选做题:习题3.33.3第第22、、44题题