2024年全等三角形难题方法归纳VIP免费

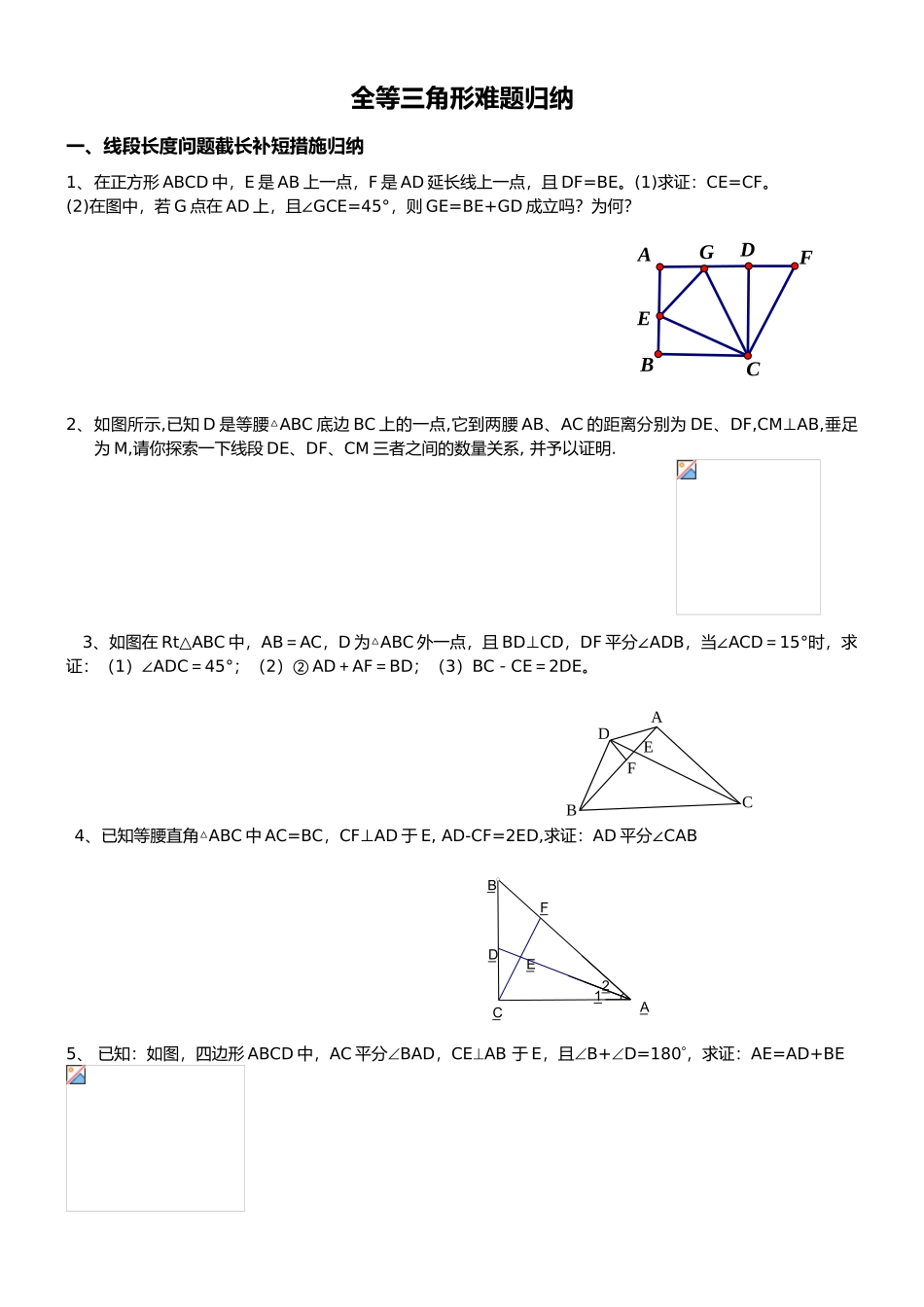
全等三角形难题归纳一、线段长度问题截长补短措施归纳1、在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。(1)求证：CE=CF。(2)在图中，若G点在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为何？2、如图所示,已知D是等腰△ABC底边BC上的一点,它到两腰AB、AC的距离分别为DE、DF,CM⊥AB,垂足为M,请你探索一下线段DE、DF、CM三者之间的数量关系,并予以证明.3、如图在Rt△ABC中，AB＝AC，D为△ABC外一点，且BD⊥CD，DF平分∠ADB，当∠ACD＝15°时，求证：（1）∠ADC＝45°；（2）②AD＋AF＝BD；（3）BC－CE＝2DE。4、已知等腰直角△ABC中AC=BC，CF⊥AD于E,AD-CF=2ED,求证：AD平分∠CAB5、已知：如图，四边形ABCD中，AC平分BAD，CEAB于E，且B+D=180，求证：AE=AD+BEADBCFEGACBDFE_A_B_C_D_E_F_1_2二、角平分线处理措施1、如图，已知AM∥BN，AC平分∠MAB，BC平分∠NBA。（1）过点C作直线DE，分别交AM、BN于点D、E，求证：AB＝AD＋BE（2）如图，若将直线DE绕点C转动，使DE与AM交于点D，与NB的延长线交于点E，则AB、AD、BE三条线段的长度之间存在何种等量关系？谫你给出结论并加以证明。2、如图，在四边形ABCD中，BD是∠ABC的角平分线，若CD＝AD，过D点作DE⊥AB，求证：AB＋BC＝2BE3、如图，已知△ABC中，AB＝AC，∠A＝100°，∠B的平分线交AC于D，求证：AD＋BD＝BC4、如图，已知△ABC中，BC＝AC，∠C＝90°，∠A的平分线交BC于D，求证：AC＋CD＝AB5、如图，已知A（0，1），B（1，0），AB=BC，A和D有关x轴对称，P为CA延长线上一动点，PE⊥CD于E，PF⊥x轴于F，求证：PF=CGABCDEACBDACBDBDACEGPFOXYABCDENMABCDMNE三、中点问题处理措施1、以的两边AB、AC为腰分别向外作等腰Rt和等腰Rt，连接DE，M、N分别是BC、DE的中点．探究：AM与DE的位置关系及数量关系．（1）如图①当为直角三角形时，AM与DE的位置关系是，线段AM与DE的数量关系是；（2）将图①中的等腰Rt绕点A沿逆时针方向旋转(0<<90)后，如图②所示，（1）问中得到的两个结论与否发生变化？并阐明理由．2、如图，AB=AD，AC=AE，∠BAD=∠CAE=90°，AH⊥BC于H，HA的延长线交DE于G。①求证：GD=GE。②若在上题中已知GD=GE其他条件不变。求证：AH⊥BCABCDEGH对应训练题1、如图，在四边形ABCD中，BD是∠ABC的角平分线，若CD＝AD，过D点作DE⊥AB，求证：AB＋BC＝2BE2、如图，已知△ABC中，CE平分∠ACB，且AE⊥CE，∠AED＋∠CAE＝180度，求证：DE∥BC3、如图，已知△ABC中，∠BAC＝90度，AD⊥BC，EF⊥BC，FM⊥AC，∠ABE＝∠CBE，求证：FM＝FD4、若D为等腰Rt△ABC的边BC上一点，且DE⊥AD，BE⊥AB，（1）求证：△ADE为等腰Rt△；（2）如图，当D在CB上任意运动时，若BC＝a，过B作BM⊥BC交AE于M，现给两个结论，①∠BMD的度数不变；②BD＋BM＋DM值不变，其中有且只有一种结论是对的的，请你判断哪一种结论对的，证明对的的结论，并求其值。ABCDEACDEBABCDEFMACBDEACBDEMF5、如图，已知在内，，，P，Q分别在BC，CA上，并且AP，BQ分别是，的角平分线。求证：BQ+AQ=AB+BP6、如图，等边△ABC和等边△CDE，A、C、E三点在一条直线上，点M为AD中点，点N为BE中点，。（1）求证：△CMN是等边三角形（2）将△CDE绕点C旋转，则下列结论发生变化吗？①AD＝BE；②AD与BE相交所成的角的度数；③△CMN为等边三角形。7、已知等腰直角△ABC中AC=BC，D是CB的中点,CF⊥AD于E,求证①∠BDF=∠ADC；②AD-CF=FDACBDEMNACEDBMN8、如图，已知在△ABC中，∠B=60°，△ABC的角平分线AD、CE相交于O点，求证：①AE＋CD=AC.②若已知AE＋CD=AC求证：∠B=60°9、如图，△ABC中∠B=90，AB=BC,D为BC上一点，AD⊥DE,AC⊥CE,求证AD=AE.10、在△ABC中，∠ACB=90°CD⊥AB，AE平分∠CAB，过F作FG∥AB交BC于G，求证：CE=BG11、在△ABC中，∠ACB=90°CD⊥AB，AE平分∠CAB，G是BC上一点且CE=BG，求证FG∥AB：12、如图A（0，2），B（﹣2，0）P为x轴上B点左边一动点，过P作PC⊥PA,且PC=PA，连CB交Y轴于D，求D点的坐标。DOCEBAACBDEABDCPOxy13、已知正方形ABCD和等腰Rt△BEF，BE=EF，∠BEF=90°，按图①放置，使点F在BC上，取DF的中点G，连接EG、CG．（1）探索EG、CG的数量关系和...