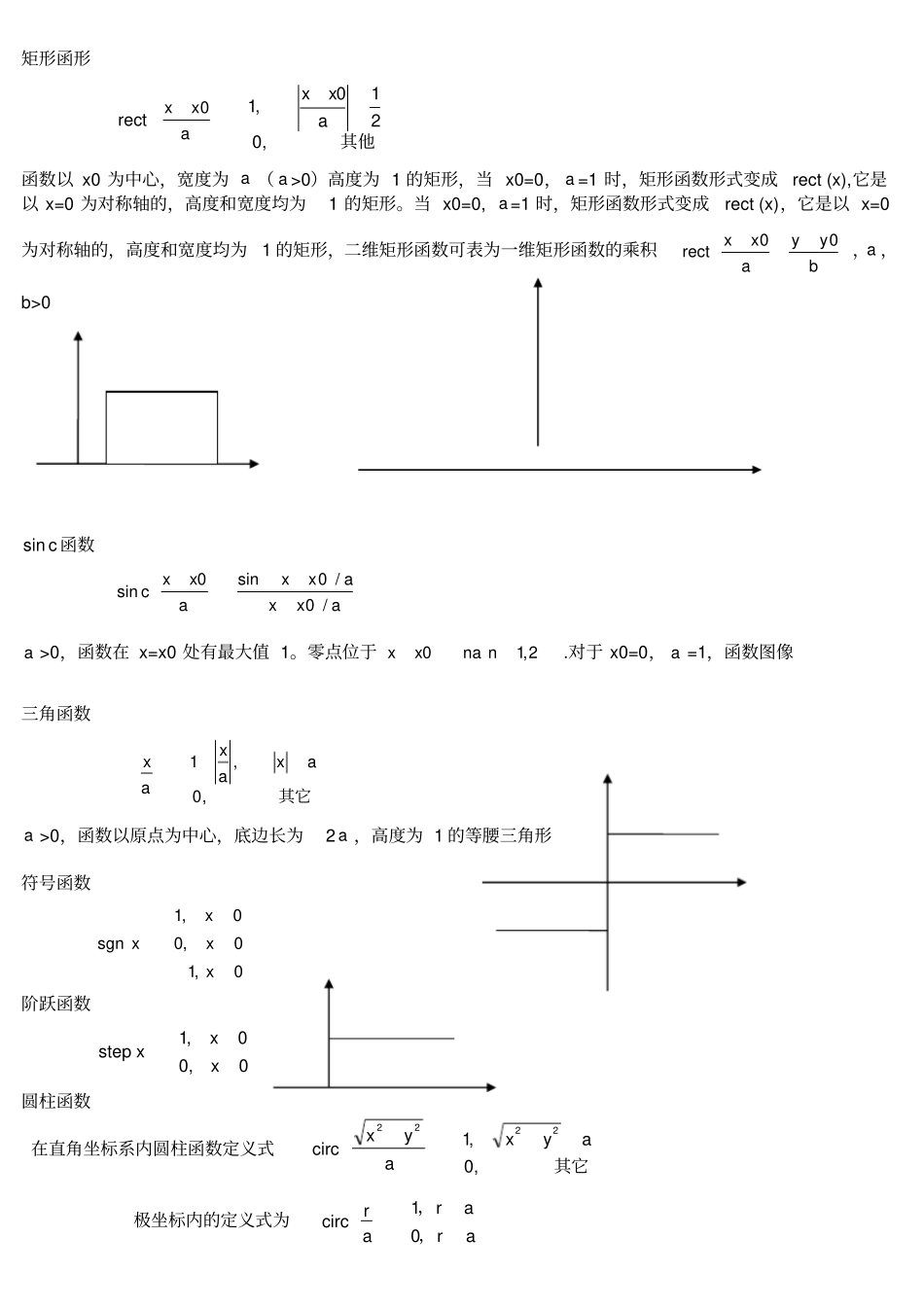
矩形函形rectaxx0其他,0210,1axx函数以x0为中心,宽度为a(a>0)高度为1的矩形,当x0=0,a=1时,矩形函数形式变成rect(x),它是以x=0为对称轴的,高度和宽度均为1的矩形。当x0=0,a=1时,矩形函数形式变成rect(x),它是以x=0为对称轴的,高度和宽度均为1的矩形,二维矩形函数可表为一维矩形函数的乘积byyaxxrect00,a,b>0csin函数axxaxxaxxc/0/0sin0sina>0,函数在x=x0处有最大值1。零点位于2,10nnaxx.对于x0=0,a=1,函数图像三角函数其它,0,1axaxaxa>0,函数以原点为中心,底边长为2a,高度为1的等腰三角形符号函数0,10,00,1sgnxxxx阶跃函数0,00,1xxxstep圆柱函数在直角坐标系内圆柱函数定义式其它,0,12222ayxayxcirc极坐标内的定义式为arararcirc,,01卷积的定义函数xf和函数xh的一维卷积,有含参变量的无穷积分定义,即xhxfdxhxfxg*定义xf和xh的二维卷积:yxhyxfddyxhfyxg,*,,,,卷积的基本性质线性性质交换律平移不变性*212121xxxgdxxhxfxxhxxf结合律坐标缩放性质axgaaxhaxf1*函数yxf,与函数的卷积yxfddyxfyxyxf,,,,*,即任意函数yxf,与函数的卷积,得出函数yxf,本身,而0000,,*,yyxxfyyxxyxf互相关两个函数yxf,和yxg,的无相关定义为含参变量的无穷积分,即yxgyxfddgyxfyxRfg,,,,,*☆或yxgyxfddyxgyxfyxRfg,,,,,*☆互相关卷积表达式:yxgyxfyxgyxf,*,,,*☆性质:(1)yxRyxRfggf,,,即互相关不具有交换性,而有yxRyxRfggf,,*(2)0,00,0,2ggfffgRRyxR自相关当yxgyxf,,时,即得到函数f的自相关定义式yxfyxfddfyxfyxRff,,,,,*☆和yxfyxfyxRff,*,,*性质:(1)自相关函数具有厄密对称性yxRyxRffff,,*当yxf,是实函数时,yxRff,是偶函数(2)0,0,ffffRyxR傅里叶变换基本性质线性性质,F,,,Gyxfbayxg,,,为常数,则,,,,gGaFyxbgyxaf对称性设,F,,yxf则,,fF迭次傅里叶变换以两次连续傅里叶为例,则有{{yxf,}}=yxf,对二元函数连续作二维傅里叶变换,即得其倒立像坐标缩放性质a,b为不等于零的实常数,若yxf,,F,则baFabbyaxf,1,函数yxf,的图像变窄,其傅里叶变换,F的图像将变宽变矮;yxf,的图像变宽,则,F的将变窄变高平移性设yxf,,F,且00,yx为实常数,则有00002exp,yxjyyxxf,F体积对应关系设yxf,,F,则有dxdyyxfF,0,0,ddyxFf,0,0复共轭函数的傅里叶变换设yxf,,F,则,,**Fyxf,,,**Fyxf若yxf,为实数,显然有,F,*F此时称,F具有厄米对称性傅里叶变换基本定理卷积定理设yxf,,F,设yxg,,G,则有yxgyxf,*,,F,G和yxgyxf,,,F,*G相关定理(维纳——辛钦定理)(1)互相关定理设yxf,,F,yxg,,G,则有yxgyxf,,☆,*F,G,*F,G为函数yxf,和yxg,的互谱量密度或简称互谱密度(2)自相关定理设yxf,,F,则有2,,,Fyxgyxf☆2,F为yxf,的能谱密度巴塞伐定理设yxf,,F,且积分设ddFdxdyyxf22,,与都存在,则有ddFdxdyyxf22,,广义巴塞伐定理设yxf,,F,yxg,,G,则有ddGFdxdyyxgyxf,,,,**导数定理设yxf,,,,,,,,,,,nmnmnmnmnmnmFFyxyxfyxfF则有nmnmjjyxf22,,,Fnmnmjjyxfyx22,,,nmF积分定理设,xfF则有FjFdfx2021矩定理2,1,0,,,nmdxdyyxfyxnm零阶矩定理此时m=n=0,即有0,0,Fdxdyyxf线性系统:一个系统同时具有叠加性和均匀性时一个系统对输入1f和2f的输出响应分别为1g和2g,即有221,yxg111,yxf,222,yxg112,yxf叠加性:112111,),(yxfyxf111,yxf+112,yxf=221,yxg222,yxg均匀性:ayxaf111,111,yxf=221,yxag线性平移不变系统:系统既具有线性又具有空间平移不变性用表达式可以表示为:单位脉冲响应输入函数输出函数yxhyxfddyxhfyxg,*,,,,线性平移不变系统的传递函数:,,,FGH说明:原点脉冲响应的频谱密度可以表征系统对输入函数中不同频率的基元成分的传递能力传递函数,H一般是复函数,其模的作用在于改变输入函数各种频率基元成分的模,其辐角的作用在于改变这些基元成分的初相位本征函数:函数yxf,满足条件yxafyxf,,式中a为一复常数,则称yxf,为算符{⋯}所表征的系统的本征函数系统的本征函数是一个特定的输入函数,相应的输出函数与输入函数之比是一个复常数平面波的空间频率:空间呈正弦或余弦变化的物理量在其某一方向上单位距离所包含的空间周期数平面波的复振幅表达式:zyxjayxjkazyxU2expcoscoscosexp,,分别沿zyx,,方...