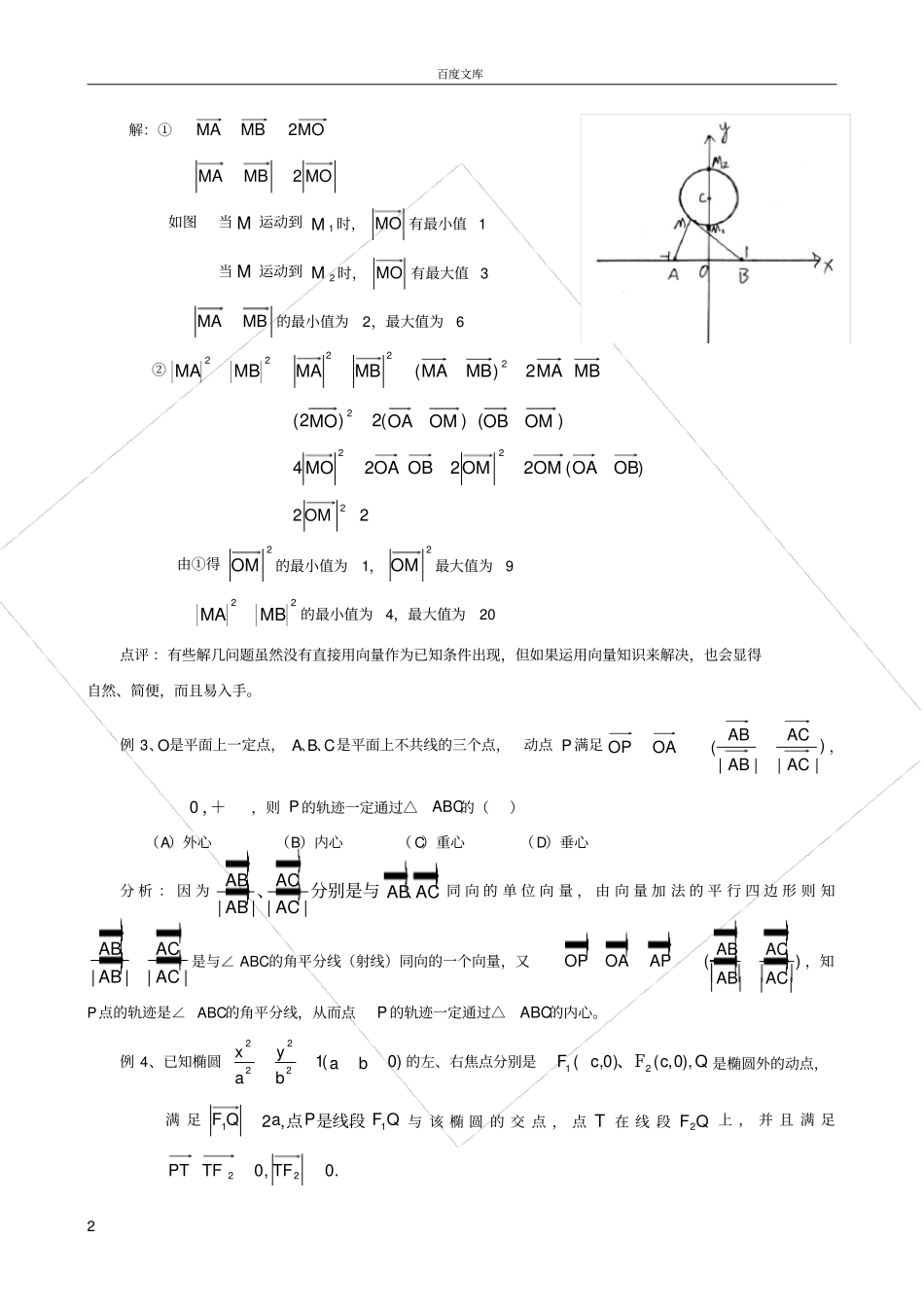
百度文库1巧用平面向量解析几何问题一:课堂教学设计:在高中数学新课程教材中,学生学习平面向量在前,学习解析几何在后,而且教材中二者知识整合的不多,很多学生在学习中就“平面向量”解平面向量题,不会应用平面向量去解决解析几何问题。用向量法解决解析几何问题思路清晰,过程简洁,有意想不到的神奇效果。著名教育家布鲁纳说过:学习的最好刺激是对所学材料的兴趣,简单的重复将会引起学生大脑疲劳,学习兴趣衰退。这充分揭示方法求变的重要性,如果我们能重视向量的教学,必然能引导学生拓展思路,减轻负担。所以本节课就这一方面做一归纳。二:教学目标:利用平面向量的加法,减法,数量积的几何意义解决解析几何问题。三:教学方法:启发式教学四:重点难点:把解析几何问题转化为向量问题。五:例题解析例1、椭圆14922yx的焦点为F,1F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是。解:F1(-5,0)F2(5,0),设P(3cos,2sin)21PFF为钝角∴1253cos,2sin)(53cos,2sin)PFPF(=9cos2-5+4sin2=5cos2-1<0解得:55cos55∴点P横坐标的取值范围是(553,553)点评:解决与角有关的一类问题,总可以从数量积入手。本题中把条件中的角为钝角转化为向量的数量积为负值,通过坐标运算列出不等式,简洁明了。例2、已知定点A(-1,0)和B(1,0),M是圆1)1(22yx上的一动点,①求MBMA的最大值和最小值;②求22MBMA的最大值和最小值分析:因为O为AB的中点,所以MOMBMA2故可利用向量把问题转化为求向量OM的最值。百度文库2解:①MOMBMA2MOMBMA2如图当M运动到1M时,MO有最小值1当M运动到2M时,MO有最大值3MBMA的最小值为2,最大值为6②MBMAMBMAMBMAMBMA2)(22222)()(2)2(2OMOBOMOAMO)(222422OBOAOMOMOBOAMO222OM由①得2OM的最小值为1,2OM最大值为922MBMA的最小值为4,最大值为20点评:有些解几问题虽然没有直接用向量作为已知条件出现,但如果运用向量知识来解决,也会显得自然、简便,而且易入手。例3、O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足)||||(ACACABABOAOP,+,0,则P的轨迹一定通过△ABC的()(A)外心(B)内心(C)重心(D)垂心分析:因为||||ABACABACABAC、分别是与、同向的单位向量,由向量加法的平行四边形则知||||ABACABAC是与∠ABC的角平分线(射线)同向的一个向量,又()ABACOPOAAPABAC,知P点的轨迹是∠ABC的角平分线,从而点P的轨迹一定通过△ABC的内心。例4、已知椭圆)0(12222babyax的左、右焦点分别是Qc、FcF),0,()0,(21是椭圆外的动点,满足QFPaQF11,2是线段点与该椭圆的交点,点T在线段QF2上,并且满足.0,022TFTFPT百度文库3(1)设x为点P的横坐标,证明xacaPF1;(2)求点T的轨迹C的方程;(3)试问:在点T的轨迹C上,是否存在点M,使21MFF的面积2bS.若存在,求21MFF的正切值;若不存在,请说明理由。(本小题主要考查平面向量的概念,椭圆的定义,椭圆的方程和性质,求轨迹的方法,以及综合运用数学知识解决问题的能力.)解:(1)证明证法一设点P的坐标为),(),(yxPyx由在椭圆上,得221)(ycxPF22222)(xabbcx2)(xaca由0acxacaa,x知,所以xacaPF1证法二设点P的坐标为),(yx记2211,rPFrPF,则221)(ycxr,222)(ycxr由,4,2222121cxrrarr得xacarPF11(2)设点),(yxT的坐标为当)0,()0,(0aa,PT和点点时在轨迹上当,TF,PT时且时002由,02时TFPT得2TFPT百度文库4又,2PFPQ所以T为线段QF2的中点.在aQFOT,FQF12121中,所以有222ayx综上所述,点T的轨迹C的方程是222ayx(3)C上存在点200),(bSyxM使的充要条件是③④由③得ay0由④得cby20所以,当cba2时,存在点,0;,22时当使cbabSM不存在满足条件的点M当cba2时,),(),,(002001yxcMFyxcMF由2222022021bcaycxMFMF212121cosMFFMFMFMFMF22121sin21bMFFMFMFS得2tan21MFF点评:本题以平面向量为载体,考查求轨迹的方法、利用方程判定曲线的性质、曲线与方程的关系例5.椭圆的中心是原点O,它的短轴长为22,相应于焦点F(c,0)(0c)的准线l与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.(1)求椭圆的方程及离心率;(2)若0OQOP,求直线PQ的方程;(3)设AQAP(1),过点P且平行于准线...