对数函数及其性质课件VIP免费

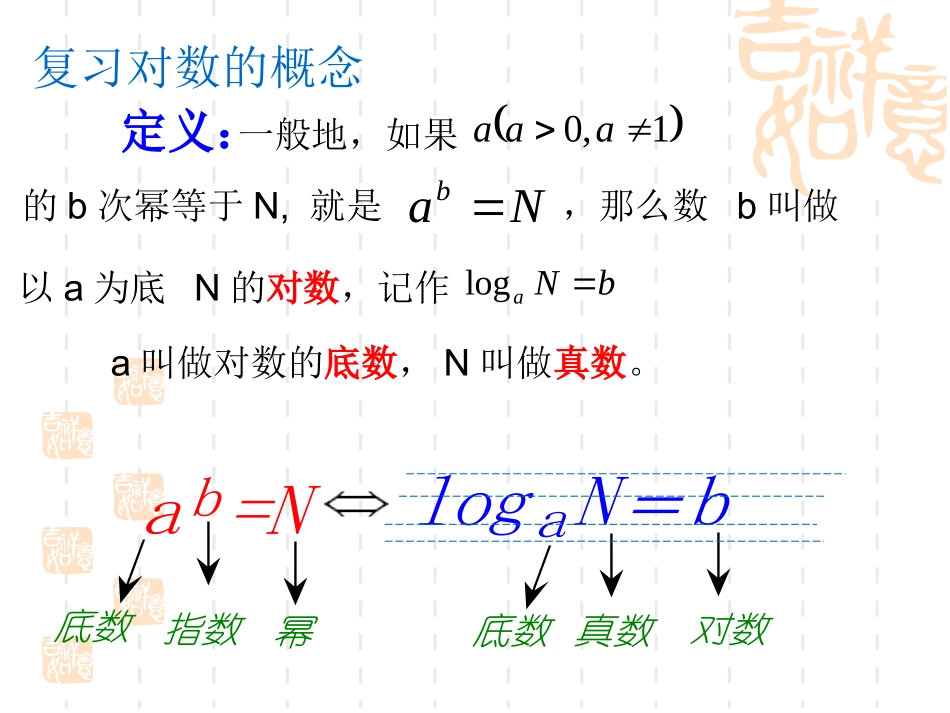
§2.2.2§2.2.2对数函数及其性质对数函数及其性质第五师89团中学黎德兵底数对数真数幂指数底数↓↓↓↓↓↓logaN＝bab=N一般地，如果1,0aaa的b次幂等于N,就是Nab，那么数b叫做以a为底N的对数，记作bNaloga叫做对数的底数，N叫做真数。复习对数的概念定义：0(logaxya)1a定义：函数，且叫做对数函数，其中x是自变量，函数的定义域是（0，+∞）。，对数函数判断：以下函数是对数函数的是（）1.y=log2(3x-2)2.y=log(x-1)x3.y=log1/3x24.y=lnx5.23log5xy4列表描点连线21-1-21240yx32114x1/41/2124xy2log221100-1-1-2-2-2-1012xy21log这两个函数的图象有什么关系呢？关于x轴对称………………y=log1/2xy=log2x思考：对数函数思考：对数函数:y=log:y=logaax(ax(a＞＞0,0,且且a≠1)a≠1)图象随着图象随着aa的取值变化图象如何变化？有规律吗？的取值变化图象如何变化？有规律吗？对数函数的图象。xyxy313loglog和猜猜:21-1-21240yx32114xy2logxy21logxy3logxy31log底大图右y=1问题：你能类比前面讨论指数函数性质的思路，提出研究对数函数性质的内容和方法吗？研究内容：定义域、值域、特殊点、单调性、最大（小）值、奇偶性．类比指数函数图象和性质的研究，研究对数函数的性质并填写如下表格：3.对数函数的图象与性质：函数y=logax(a＞0且a≠1)底数a＞10＜a＜1图象定义域奇偶性值域定点单调性函数值符号1xyo1xyo非奇非偶函数非奇非偶函数(0,+∞)R(1,0)即x=1时，y=0在(0,+∞)上是增函数在(0,+∞)上是减函数当x＞1时，y＞0当0＜x＜1时，y＜0当x＞1时，y＜0当0＜x＜1时，y＞0例1:求下列函数的定义域:(1)y=logax2(2)y=loga(4-x)解:(1)因为x2>0,所以x≠,即函数y=logax2的定义域为-(0,+(2)因为4-x>0,所以x<4,即函数y=loga(4-x)的定义域为(-4)例1中求定义域时应注意：①对数的真数大于0，底数大于0且不等于1；②使式子符合实际背景；③对含有字母的式子要注意分类讨论。例2比较下列各组数中两个值的大小：⑴log23.4,log28.5⑵log0.31.8,log0.32.7⑶loga5.1,loga5.9(a＞0,a≠1)解⑴考察对数函数y=log2x,因为它的底数2＞1所以它在(0,+∞)上是增函数,于是log23.4＜log28.5⑵考察对数函数y=log0.3x,因为它的底数0.3,即0＜0.3＜1,所以它在(0,+∞)上是减函数,于是log0.31.8＞log0.32.7对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件中并未指出底数a与1哪个大,因此需要对底数a进行讨论:当a＞1时,函数y=logax在(0,+∞)上是增函数,于是loga5.1＜loga5.9当0＜a＜1时,函数y=logax在(0,+∞)上是减函数,于是loga5.1＞loga5.9⑶loga5.1,loga5.9(a＞0,a≠1)注注::例例22是利用对数函数的增减性比较两是利用对数函数的增减性比较两个对数的大小的个对数的大小的,,对底数与对底数与11的大小关系未明确指出的大小关系未明确指出时时,,要分情况对底数进行讨论来比较两个对数的大要分情况对底数进行讨论来比较两个对数的大小小.例3比较下列各组中两个值的大小:⑴.log67,log76;.log⑵3π,log20.8.解:⑴∵log67＞log66＝1log76＜log77＝1∴log67＞log76⑵∵log3π＞log31＝0log20.8＜log21＝0∴log3π＞log20.8注注::例例33是利用对数函数的增减性比较两个对数的大小是利用对数函数的增减性比较两个对数的大小..当不能直接进行比较时当不能直接进行比较时,,可在两个对数中间插入一可在两个对数中间插入一个已知数个已知数((如如11或或00等等),),间接比较上述两个对数的间接比较上述两个对数的大小大小..131log).3()32(log2).2()13(log).1(.13245.0xxyxxyxy求下列函数的定义域例.32,31x.Rx.311xxxx或}311|{3110)13)(1(0131131log).3(02)1(32)32(log2).2(}3231|{32311130131log0)13(log013)13(log).1(322245.05.05.0xxxxxxxxxxxxyRxxxxxxyxxxxxxxxxy或或解：解：解：.loglog)2(;loglog)1(:,1.311cbcbcbaaaaa和和比较下列各组数的大小已知.1,0,3log2log)4(;3log2log)3(;7.0log8.0log)2(;7.0log8.0log)1(:.255212144aaaa其中和和和和比较下列各组数的大小小结（1）本节要求掌握对数函数的概念、图象和性质．（2）在理解对数函数的定义的基础上，掌握对数函数的图象和性质的应用是本小节的重点．2(1)axax函数f(x)=log的定义域为R，2求的取值范围？想一想：作业：P74习题2.2A组第7、8题