计量经济学计算机作业VIP免费

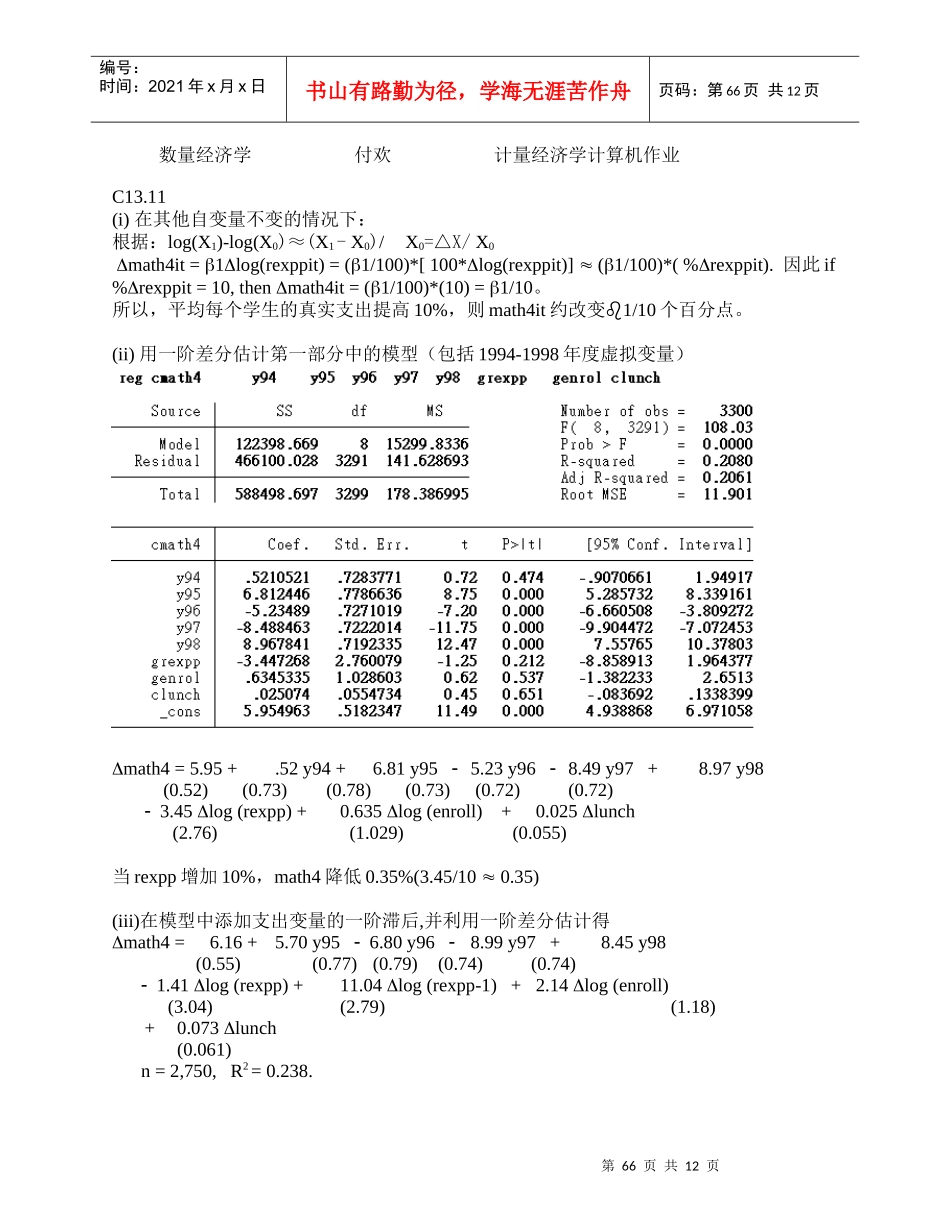
第66页共12页编号：时间：2021年x月x日书山有路勤为径，学海无涯苦作舟页码：第66页共12页数量经济学付欢计量经济学计算机作业C13.11(i)在其他自变量不变的情况下：根据：log(X1)-log(X0)≈(X1-X0)/X0=△X/X0math4it=1log(rexppit)=(1/100)*[100*log(rexppit)](1/100)*(%rexppit).因此if%rexppit=10,thenmath4it=(1/100)*(10)=1/10。所以，平均每个学生的真实支出提高10%，则math4it约改变1/10个百分点。(ii)用一阶差分估计第一部分中的模型（包括1994-1998年度虚拟变量）math4=5.95+.52y94+6.81y955.23y968.49y97+8.97y98(0.52)(0.73)(0.78)(0.73)(0.72)(0.72)3.45log(rexpp)+0.635log(enroll)+0.025lunch(2.76)(1.029)(0.055)当rexpp增加10%，math4降低0.35%(3.45/100.35)(iii)在模型中添加支出变量的一阶滞后,并利用一阶差分估计得math4=6.16+5.70y956.80y968.99y97+8.45y98(0.55)(0.77)(0.79)(0.74)(0.74)1.41log(rexpp)+11.04log(rexpp-1)+2.14log(enroll)(3.04)(2.79)(1.18)+0.073lunch(0.061)n=2,750,R2=0.238.第67页共12页第66页共12页编号：时间：2021年x月x日书山有路勤为径，学海无涯苦作舟页码：第67页共12页回归图如下由回归图所示：即期支出变量的系数为-1.41，t统计量为-0.46，统计上不显著滞后支出变量的系数为11.04，t统计量为3.96，统计上显著(iv)第68页共12页第67页共12页编号：时间：2021年x月x日书山有路勤为径，学海无涯苦作舟页码：第68页共12页比较：的异方差稳健标准误为4.28，从而降低了log(rexpp)的统计显著性的异方差稳健标准误为4.38，其t统计量降低为2.52。在1%的显著性水平双侧检验下log(rexpp-1)仍然是统计显著的。(t统计量大于1.96)(v)异方差序列相关稳健标准误为4.94，log(rexpp)的t统计量降低了。的标准误为5.13,log(rexpp-1)的t统计量为2.15.双侧检验的p值为0.032(vi)使用1995,1996,1997,1998年进行混合的OLS可得0.423这表明差分误差有很强的负序列相关(vii)基于充分稳健的联合检验，如下图log()ˆrexpp1log()ˆrexpplog()ˆrexpp1log()ˆrexppˆ第69页共12页第68页共12页编号：时间：2021年x月x日书山有路勤为径，学海无涯苦作舟页码：第69页共12页所以模型中没有必要包含学生注册的人数和午餐项目变量C14.10(i)根据回归可知利用混合OLS估计的β1=0.36,当Δconcen=0.10，则Δlfare=0.36*0.10=0.036.airfare增加3.6%、(ii)β1的95%的置信区间为[0.309,0.419]只有当复合误差序列无关，得出的标准误才是有效的,所以有点不太可能，充分稳健下的95%的置信区间为[0.245,0.475],条件为允许存在序列相关和异方差,所以充分稳健下的置信区间比一般的置信区间要大。忽略序列相关会导致参数估计产生不确定性.(iii).斜率变为正斜率的log(fare)的值为0.902/[2*0.103]≈4.38。dist的值为exp(4.38)=80.。该值表示的是fare对dist的正弹性系数。(iv)β1的RE估计值为0.209，表示fare与concern之间正相关。因为t=7.88估计值统计上显著第70页共12页第69页共12页编号：时间：2021年x月x日书山有路勤为径，学海无涯苦作舟页码：第70页共12页(v)FE估计值为0.169，RE的λ估计值为0.9.我们可以预计RE估计值与FE估计值非常相似。第71页共12页第70页共12页编号：时间：2021年x月x日书山有路勤为径，学海无涯苦作舟页码：第71页共12页(vi)在一个航班线上的两个机场附近的城市影响航行的因素为人口，教育水平，雇主类型等。高速路及铁路的便利情况及周围的地理环境，可以考虑为固定不变的。这些因素和concern相关。(vii)考虑到无法观测效应，我们可以使用固定效应模型得出估计值为正，且统计上显著。用FE估计得到的估计值为0.169concern与时间常量正相关C15.8(i)Ftestthatallu_i=0:F(1148,3443)=36.90Prob>F=0.0000rho.94316439(fractionofvarianceduetou_i)sigma_e.10651186sigma_u.43389176_cons4.953331.0182869270.870.0004.9174764.989185ldistsq(omitted)ldist(omitted)concen.168859.02941015.740.000.1111959.226522y00.0977717.004455521.940.000.089036.1065073y99...