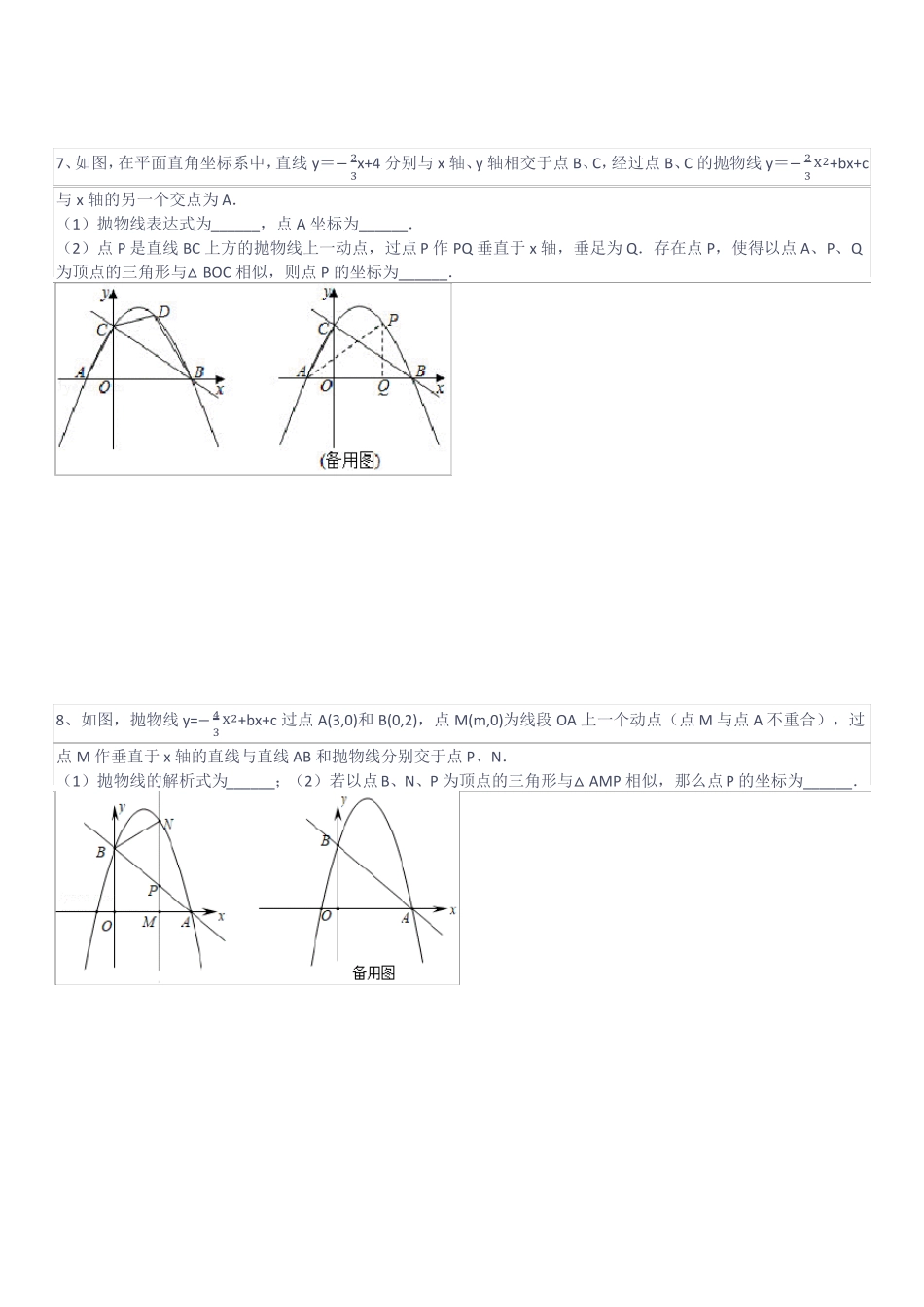
一、相似三角形的存在性二次函数下“两边一夹角”型相似三角形的存在性的解题思路(1)假设存在,分类讨论;(2)从“角”入手,是否有固定相等的角(3)利用二次函数,表示出线段长(4)对应边成比例,求点的坐标.1、如图1,已知抛物线y=(x+1)(x﹣3)(m为常数,且m>0)经过点C(0,﹣√3),与x轴交于点A、B3𝑚(点A位于点B的左侧).(1)m的值为______,点B的坐标为______;(2)在直线BC上存在点P,使以P、A、B为顶点的三角形与△BOC相似,AP的长为______.2、如图,已知一次函数y=kx+b的图象经过A(﹣1,﹣5),B(0,﹣4)两点且与x轴交于点C,二次函数y=ax2+bx+4的图象经过点A、点C.(1)一次函数的函数表达式为______;二次函数的函数表达式为______;(2)若点D在x轴的正半轴上,存在以点D,C,B构成的三角形与△OAB相似,点D的坐标为______3、如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点E.(1)抛物线解析式为______,点D的坐标为______;(2)抛物线上B,D之间存在一点M,过点M作MN⊥CD交直线CD于点N,以C,M,N为顶点的三角形与△BDE相似,点M的坐标为______.4、已知,在平面直角坐标系中,直线l与y轴相交于点A(0,m),其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)经过点B,它与直线l相交于另一点C.(1)若AC:BC=1:3,a的值(用含m的代数式表示)为______;(2)在(1)的条件下,若抛物线的顶点为F,其对称轴与直线l和x轴分别相交于点D、E,当以F、C、D为顶点的三角形与△BED相似时,抛物线的函数表达式为______5、如图,在平面直角坐标系xOy中,顶点为M的抛物线C1:y=ax2+bx(a<0)经过点A和x轴上的点B,AO=OB=2,∠AOB=120∘.(1)抛物线的表达式为______;(2)将抛物线C1向上平移得到抛物线C2,抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果M、B、F为顶点的三角形与ΔAOM相似,则F点的坐标为______.6、设抛物线y=ax2+bx﹣2与x轴交于两个不同的点A(﹣1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.(1)抛物线的解析式为______;(2)已知过点A的直线y=x+1交抛物线于另一点E,且点D(1,﹣3)在抛物线上,在x轴上存在点P,使以点P、B、D为顶点的三角形与△AEB相似,点P的坐标为______.7、如图,在平面直角坐标系中,直线y=−3x+4分别与x轴、y轴相交于点B、C,经过点B、C的抛物线y=−3x2+bx+c与x轴的另一个交点为A.(1)抛物线表达式为______,点A坐标为______.(2)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似,则点P的坐标为______.228、如图,抛物线y=−x2+bx+c过点A(3,0)和B(0,2),点M(m,0)为线段OA上一个动点(点M与点A不重合),过34点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.(1)抛物线的解析式为______;(2)若以点B、N、P为顶点的三角形与△AMP相似,那么点P的坐标为______.9、如图,抛物线y=−2x2+2x+2与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.(1)点A的坐标为______;点B的坐标为______;点C的坐标为______;(2)点P在线段AB上运动过程中,存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似,点Q的坐标为______.1310、如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴对折,点A落到点C处,过点A、B的抛物线y=﹣𝑥2+bx+c与直线BC交于点B、D.(1)抛物线的解析式为______;(2)在第一象限内的抛物线上,存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为项点的三角形与△BOC相似,点M的坐标为______.11、如图,抛物线y=ax2+2x+c经过A(﹣1,0),B两点,且与y轴交于点C(0,3),抛物线与直线y=﹣x﹣1交于A,E两点.(1)抛物线的解析式为______;(2)P点在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标______.12、如图,抛物线y=−x2+bx+c与x轴分别交于点A(﹣1,0...