相似三角形复习课件VIP免费

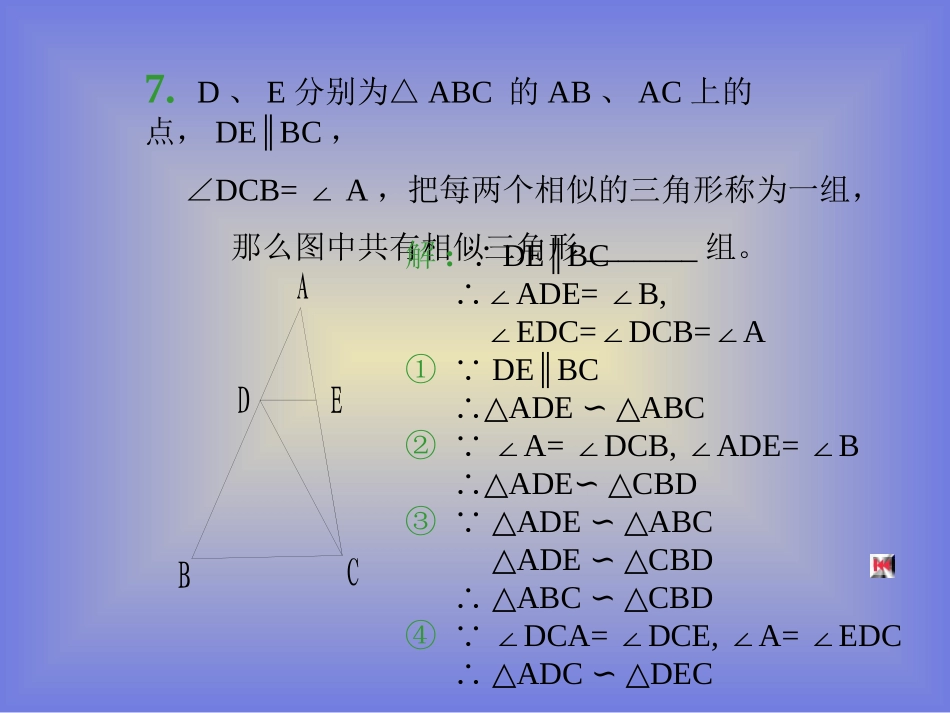
<<相似三角形的判定>><<相似三角形的判定>>复习课复习课二、证明题：1.D为△ABC中AB边上一点，∠ACD=ABC.∠求证：AC2=AD·AB.2.ABC△中,BAC∠是直角，过斜边中点M而垂直于斜边BC的直线交CA的延长线于E，交AB于D，连AM.求证：①△MAD～△MEA②AM2=MD·ME3.如图，ABCD∥，AO=OB，DF=FB，DF交AC于E，求证：ED2=EO·EC.ABCDABCDEMABCDEFO7.D、E分别为△ABC的AB、AC上的点，DEBC∥，∠DCB=A∠，把每两个相似的三角形称为一组，那么图中共有相似三角形_______组。ABEDC解:DEBC∵∥∴∠ADE=B,∠∠EDC=DCB=A∠∠①∵DEBC∥∴△ADEABC∽△②∵∠A=DCB,ADE=B∠∠∠∴△ADECBD∽△③∵△ADEABC∽△△ADECBD∽△∴△ABCCBD∽△④∵∠DCA=DCE,A=EDC∠∠∠∴△ADCDEC∽△3.如图，ABCD∥，AO=OB，DF=FB，DF交AC于E，求证：ED2=EO·EC.ABCDEFO分析：欲证ED2=EO·EC，即证：，只需证DE、EO、EC所在的三角形相似。EDEO=ECED证明：∵ABCD∥∴∠C=A∠∵AO=OB，DF=FB∴∠A=B∠，∠B=FDB∠∴∠C=FDB∠又∵∠DEO=DEC∠∴△EDCEOD∽△∴，即ED2=EO·ECEDEO=ECED4.过◇ABCD的一个顶点A作一直线分别交对角线BD、边BC、边DC的延长线于E、F、G.求证：EA2=EF·EG.ABCDEFG分析：要证明EA2=EF·EG，即证明成立，而EA、EG、EF三条线段在同一直线上，无法构成两个三角形，此时应采用换线段、换比例的方法。可证明：△AEDFEB∽△，△AEBGED.∽△EAEG=EFEA证明：∵ADBFABBC∥∥∴△AEDFEB∽△△AEBGED∽△∴∴EAEG=ABDGEFEA=BEED=ABDGEAEG=EFEA5.ABC△为锐角三角形，BD、CE为高.求证：△ADEABC∽△（用两种方法证明）.证明一：∵BDAC⊥，CEAB⊥∴∠ABD+A=90°∠，∠ACE+A=90°∠∴∠ABD=ACE∠又∵∠A=A∠∴△ABDACE∽△∴∵∠A=A∠∴△ADEABC∽△ADAE=ABAC证明二：∵∠BEO=CDO∠∠BOE=COD∠∴△BOECOD∽△∴即又∵∠BOC=EOD∠∴△BOCEOD∽△∴∠1=2∠∵∠1+BCD=90°∠，∠2+3=90°∠∠∴∠BCD=3∠又∵∠A=A∠∴△ADEABC∽△ODOEOCOBODOCOEOB1O23ABCDE1.已知：如图，△ABC中，P是AB边上的一点，连结CP．满足什么条件时△ACPABC∽△．解:A=A⑴∵∠∠，∴当∠1=ACB∠（或∠2=B∠）时，△ACPABC∽△⑵∵∠A=A∠，∴当AC:AP＝AB:AC时，△ACPABC∽△⑶∵∠A=A∠，当∠4＋∠ACB＝180°时，△ACPABC∽△答：当∠1=ACB∠或∠2=B∠或AC:AP＝AB:AC或∠4＋∠ACB＝180°时,ACPABC.△∽△APBC1241、条件探索型三、探索题2.如图：已知∠ABC＝∠CDB＝90°，AC＝a，BC=b，当BD与a、b之间满足怎样的关系式时，两三角形相似DABCab解:⑴∵1∠＝∠D＝90°∴当时，即当时，△ABCCDB,∴∽△⑵∵∠1＝∠D＝90°∴当时，即当时，△ABCBDC∽△，∴答：略.BDBCBCACBDbbaBDABBCACBDbaba22abBD2ababBD22１这类题型结论是明确的，而需要完备使结论成立的条件．解题思路是：从给定结论出发，通过逆向思考寻求使结论成立的条件．1.将两块完全相同的等腰直角三角板摆成如图的样子，假设图形中的所有点、线都在同一平面内，则图中有相似（不包括全等）三角形吗？如有，把它们一一写出来.C解：有相似三角形，它们是：△ADEBAE,BAE∽△△∽CDA△，△ADECDA∽△（△ADEBAECDA∽△∽△）2、结论探索型ABDEGF１22.△在ABC中，AB>AC，过AB上一点D作直线DE交另一边于E，使所得三角形与原三角形相似，画出满足条件的图形.EDABCDABCDABCDABCEEE这类题型的特征是有条件而无结论，要确定这些条件下可能出现的结论．解题思路是：从所给条件出发，通过分析、比较、猜想、寻求多种解法和结论，再进行证明.3、存在探索型如图,DE是△ABC的中位线，在射线AF上是否存在点M，使△MEC与△ADE相似,若存在,请先确定点M,再证明这两个三角形相似，若不存在，请说明理由.ADBCEF证明：连结MC，∵DE是△ABC的中位线，∴DEBC∥，AE＝EC，又∵MEAC,⊥∴AM＝CM，∴∠1=2∠，∵∠B=90°，∴∠4＝∠B=90°，∵AFBC∥，AMDE,∥∴∠1=2∠，∴∠3=2,∠∵∠ADE＝∠MEC=90°，∴△ADEMEC∽△．ADBCEF123M解:存在.过点E作AC的垂线,与AF交于一点,即M点(或作∠MCA=AED).∠4所谓存在性问题，一般是要求确定满足某些特定要求的元素有或没有的问题．解题思路是：先假定所需探索的对象存在或结论成立，以此为依据进行计算或推理，若由此推出矛盾，则假定是错误的，从而给出否定的结论，否则给出肯定的证明．