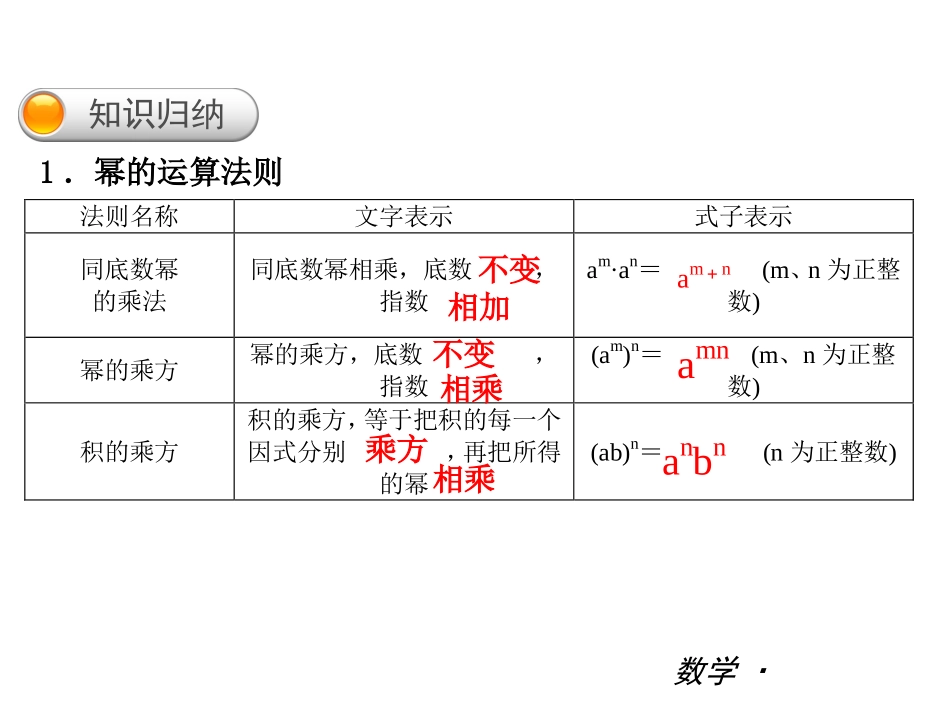
第十二章|复习(一)知识归纳数学·人教版(RJ)法则名称文字表示式子表示同底数幂的乘法同底数幂相乘,底数,指数am·an=(m、n为正整数)幂的乘方幂的乘方,底数,指数(am)n=(m、n为正整数)积的乘方积的乘方,等于把积的每一个因式分别,再把所得的幂(ab)n=(n为正整数)不变相加不变相乘乘方相乘am+namnanbn1.幂的运算法则第十二章|复习(一)数学·人教版(RJ)同底数幂的除法同底数幂相除,底数,指数am÷an=(a≠0,m、n为正整数,且m>n)相同点运算中的不变,只对作运算不同点(1)同底数幂相乘是指数;(2)幂的乘方是指数;(3)积的乘方是每个因式分别;(4)同底数幂相除是指数相加相乘乘方相减底数指数不变相减am-n第十二章|复习(一)数学·人教版(RJ)[注意](1)其中的a、b代表的不仅可以是单独的数、单独的字母,还可以是一个任意的代数式;(2)这几个法则容易混淆,计算时必须先搞清楚该不该用法则、该用哪个法则.2.整式的乘法单项式与单项式相乘,把它们的、分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个.单项式与多项式相乘,用和的每一项分别相乘,再把所得的积.多项式与多项式相乘,先用一个多项式的与另一个多项式的相乘,再把所得的积.系数相同字母的幂因式单项式多项式相加每一项每一项相加第十二章|复习(一)数学·人教版(RJ)3.乘法公式公式名称两数和乘以这两数的差两数和(差)的平方文字表示两数和与这两数的差的积,等于这两数的平方差两数和(差)的平方,等于这两数的加上(减去)的2倍平方和这两数积式子表示(a+b)(a-b)=(a±b)2=a2-b2a2±2ab+b2第十二章|复习(一)数学·人教版(RJ)结构特点①左边是两个项式相乘,这两个二项式中有一项,另一项;②右边是项式,是乘式中两项的,即相同项的平方与相反项的平方的差①左边是一个项式的和(或差)的;②右边是项式,是左边二项式中两项的,再(或减去)它们的2倍顺口溜和差积,平方差首平方,尾平方,首尾倍中间放,加减看前方,同加异减二完全相同互为相反数二平方差二平方三平方和加上积两第十一章|复习数学·人教版(RJ)公式的常用变形a2=(a-b)+b2;b2=-(a+b)(a-b)a2+b2=(a+b)2-或(a-b)2+;(a+b)2=(a-b)2+(a+b)a22ab2ab4ab[点拨](1)乘法公式实际上是一种特殊形式的多项式的乘法,公式的主要作用是简化运算;(2)公式中的字母可以表示数,也可以表示其他单项式或多项式.第十二章|复习(一)数学·人教版(RJ)4.整式的除法(1)单项式除以单项式单项式相除,把、分别相除作为商的,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个.(2)多项式除以单项式多项式除以单项式,先把这个多项式的每一项除以这个,再把所得的商.[点拨]多项式除以单项式实质上是用计算法则转化为单项式除以单项式.系数同底数幂因式因式单项式相加第十二章|复习(一)考点攻略数学·人教版(RJ)考点一同底数幂的乘法计算a2·a3的结果是()A.2a6B.2a5C.a6D.a5D[解析]D根据am·an=am+n,知道a2·a3=a5,所以选D.易错警示(1)法则“同底数幂相乘,底数不变,指数相加”易被误记为“指数相乘”;(2)同底数幂的加法与乘法容易混淆,an+an=2an,而an·an=a2n.第十二章|复习(一)数学·人教版(RJ)考点二幂的乘方例2计算(a3)2·a3的结果是()A.a8B.a9C.a10D.a11B[解析]B本题先用幂的乘方法则计算(a3)2,再用同底数幂的乘法法则得到最后的结果.易错警示幂的乘方法则中的“指数相乘”容易被误记为“指数相加”.第十二章|复习(一)数学·人教版(RJ)考点三积的乘方计算-(-3a2b3)4的结果是()A.81a8b12B.12a6b7C.-12a6b7D.-81a8b12D[解析]D根据积的乘方法则可得:-(-3a2b3)4=-(-3)4(a2)4(b3)4=-81a8b12.所以选D.易错警示同底数幂的乘法与积的乘方易混淆,am·an=am+n,(ab)n=anbn.第十二章|复习(一)数学·人教版(RJ)考点四同底数幂的除法例4下列运算正确的是()A.a6÷a2=a6÷2=a3B.x3÷x2=x3-2=xC.(-a)2×a3÷a3=a2×(a3÷a3)=a2D.(-0.25)2012×42013=-4×(0.25×4)2012=-4B[解析]B选项A中误把指数相减当作指数相除;...