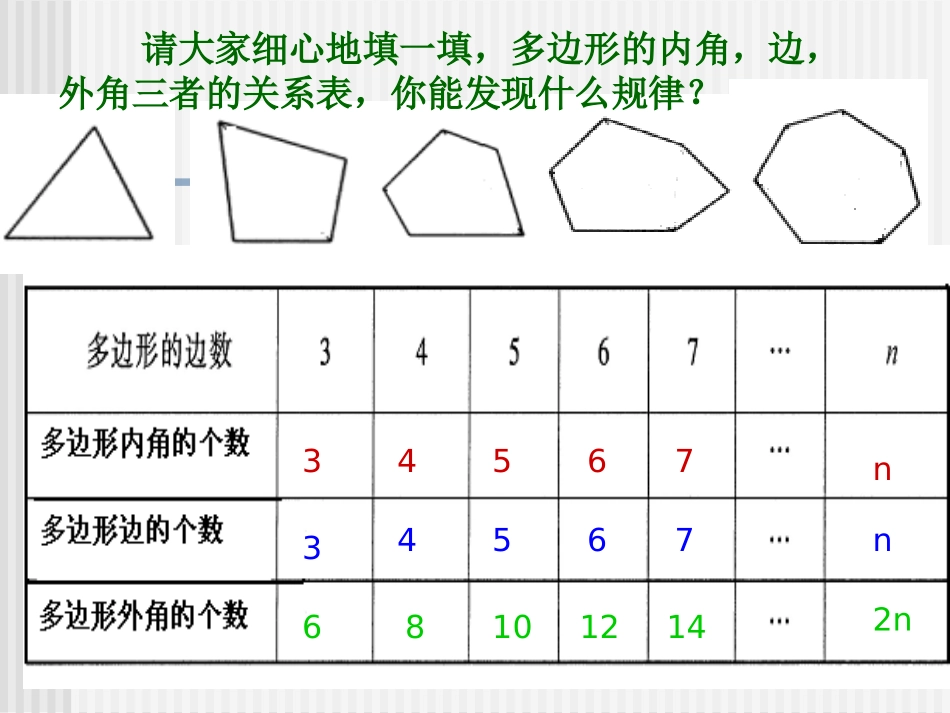
请大家细心地填一填,多边形的内角,边,外角三者的关系表,你能发现什么规律?3344556677nn681012142n三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形。如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。如正三角形、正四边形(正方形)、正五边形等等。正三角形正四边形正五边形正六边形正八边形(或正三边形)(或正四边形)例1.求八边形的内角和的度数.解(n-2)×180°=(8-2)×180°=1080°分析:n边形的内角和公式为(n-2)180°,现在知道这个多边形的边数是,代入这个公式既可求出.老师,可以用计算器吗?例2.已知多边形的内角和的度数为900°,则这个多边形的边数为________解(n-2)×180°=900°(n-2)=900°/180°(n-2)=5n=5+2n=77哇!这么简单呀!例3.已知在一个十边形中,九个内角的和的度数是1290°,求这个十边形的另一个内角的度数.解:(10-2)×180°=1440°则十边形的另一个内角的度数为1440°-1290°=150°先求出十边形的内角和再减去1290°,就可以得出.那么对于正多边形来说,又遇到怎样的问题呢?因为正多边形的每个角相等,所以知道正多边形的边数,就可以求出每一个内角的度数.(n-2)×180°/n例4.正五边形的每一个内角等于_____,外角等于___.例5.如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____解:(n-2)×180°/n=(5-2)×180°/5=540°/5=108°解:120°n=(n-2)×180°120°n=n×180°-360°60°n=360°n=6例5.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____A.12B.9C.8D.7A例7.如果一个多边形的边数增加1,则这个多边形的内角和_____增加180°例6.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____解;设五边形中前四个角的度数分别是x,2x,3x,4x,则第五个角度数是x+100°.X+2x+3x+4x+x+100°=(5-2)×180°11X+100°=540°11X=440°X=40°则这个五边形的内角分别为40,80°,120°,160°,140°.例8.五边形中,前四个角的比是1:2:3:4,第五个角比最小角多100°,则这个五边形的内角分别为_____请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?23456n-1180°360°540°720°900°180°(n-1)-180°2.从边上的一个点出发请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?34567n180°360°540°720°900°180°n-360°3.从多边形内一个点出发请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?180°n-360°=180°n-2X180°=180°(n-2)4.从多边形外一个点出发前面我们学习了三角形的外角和是360°,当时是怎样研究出来的?ABCDEF1.先把三角形的三个外角和三个内角这六个角的和求出来,刚好是三个平角。2.再用这六个角的和减去三个内角的和,剩下的就是三角形的外角和了!图8.3.6那么你能研究出四边形的外角和吗?整体思路:1.先求4个外角+4个内角的和;2.再减去4个内角的和容易看出,4个外角+4个内角=4个平角而4个内角的和是360°,那么四边形的外角和就是4X180°-360°=360°那么出五边形,六边形,n边形的外角和吗?五边形的外角和就是5X180°-540°=360°六边形的外角和就是6X180°-720°=360°。。。。。。n边形的外角和就是nX180°-(n-2)X180°=(n-n+2)X180°=360°任意多边形的外角和都为360°例9.正五边形的每一个外角等于___.每一个内角等于_____,72°144°例10.如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____6例11.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____A.12B.9C.8D.7A例12.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____12例13.一个正多边形的一个内角和是外角和的2倍,则这个多边形为()A.三角形B.四边形C.五边形D.六边形例14.一个正多边形的一个内角和与外角和的比是7:2,则这个多边形的边数为()思考一:一个三角形中,它的内角最多可以有几个锐角?为什么?思考二:一个四边形中,它的内角最多可以有几个锐角?为什么?思考三:一个多边形中,它的内角最多可以有几个锐角?为什么?一个多边形中,它的外角最多可以有几个钝角?3与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和