旋转体中的内接几何体VIP免费

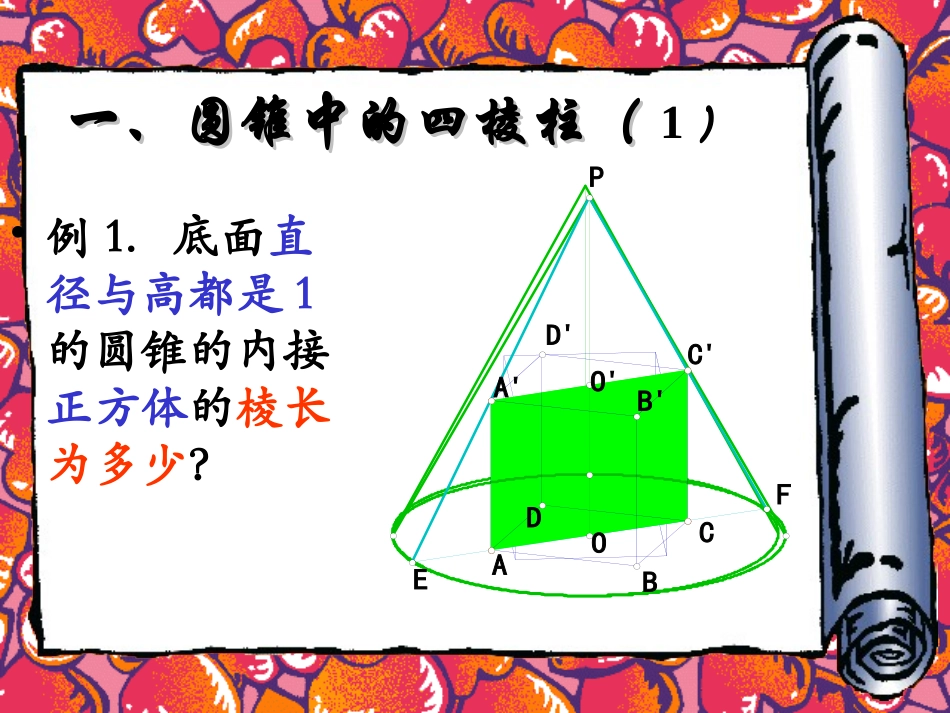
旋转体中的内接几何体旋转体中的内接几何体（一）（一）------------圆锥中的内接正棱柱圆锥中的内接正棱柱一、圆锥中的四棱柱（一、圆锥中的四棱柱（1）•例1.底面直径与高都是1的圆锥的内接正方体的棱长为多少？OPO'DAED'A'BCFB'C'略解略解由轴截面可知设正方体的棱长为,x,xCCAAOOxOP1则EFCAPOOPEFCA//1211xx12121xCAC'A'O'EFOP1,1EFPO,2xACCA二、圆锥中的四棱柱（二、圆锥中的四棱柱（22）•例2.求底面半径为r，高为d的圆锥的内接正四棱柱的侧面积的最大值。OPO'DAED'A'BCFB'C'略解略解hx高为为设正四棱柱的底面边长,,由轴截面可知,2xCA则,hOO,2rEF,dPOhdOPEFCAPOOPEFCA//rxdhd2:2:)(dhdrx)(2hdhdrxhS)(244側面积)(242hdhdr]4)2([2422ddhdr,2时当dhdrddrS24242maxdh0CAC'A'O'EFOP三、圆锥中的三棱柱三、圆锥中的三棱柱•例3.求底面半径为4cm，高为12cm的圆锥的内接正三棱柱的表面积的最大值。OPBB'CAA'C'EFO'略解略解EPOFO'A'AD'Dhx高为为设正三棱柱的底面边长,4,12,OFOEPO由轴截面可知,23xDAAD则,33xOAAO340,4330xxAOOA//AOOAPOOP4331212xhxh31224323xxhS表面积223)312(3xxxxx3623525216)5312(2352x2maxcm5216,cm5312Sx当hOP12思考与练习思考与练习•11、圆锥底面、圆锥底面半径半径rr，，高为高为hh，内接，内接一正三棱柱，且该正三棱柱一正三棱柱，且该正三棱柱侧面是侧面是正方形正方形，求三棱柱的，求三棱柱的側棱长側棱长。。•22、求底面、求底面半径为半径为5cm5cm，，高为高为12c12cmm的圆锥的内接正三棱柱的的圆锥的内接正三棱柱的侧面积侧面积的最大值的最大值。。rhhr33:1题答案第2cm39:2题答案第四、课堂小结四、课堂小结•一、圆锥中的内接正棱柱的“一、圆锥中的内接正棱柱的“内内接接”概念。”概念。•二、寻找二、寻找合适的合适的轴截面位置，建立轴截面位置，建立相似比。相似比。•三、建立三、建立目标函数目标函数，求最值。，求最值。