垂径定理小结与练习VIP免费

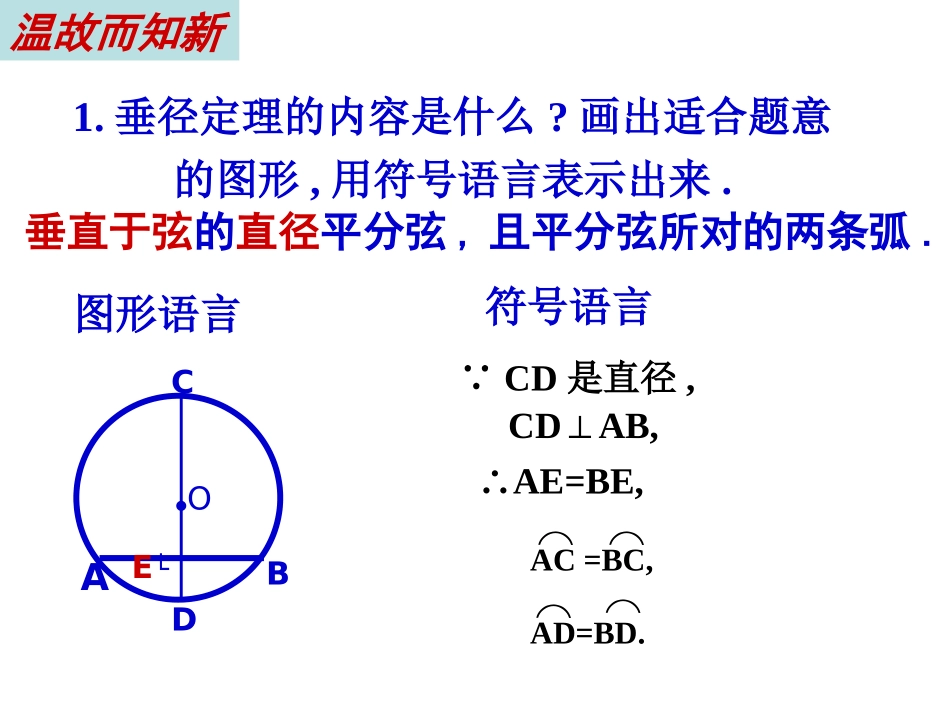
垂径定理小结与练习1.垂径定理的内容是什么?画出适合题意的图形,用符号语言表示出来.垂直于弦的直径平分弦,且平分弦所对的两条弧.●OABCDE└CDAB,⊥∵CD是直径,∴AE=BE,⌒⌒AC=BC,⌒⌒AD=BD.符号语言图形语言温故而知新垂径定理推论平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧。∴CD⊥AB,∵CD是直径，AE=BE⌒⌒AC=BC,⌒⌒AD=BD.·OABCDEEDCOABOBCADDOBCAOBAC垂径定理的几个基本图形：CD过圆心CD⊥AB于EAE=BEAC=BCAD=BDEDCOAB下列图形是否具备垂径定理的条件？ECOABDOABc是不是是不是OEDCAB1、两条辅助线：半径、圆心到弦的垂线段2、一个Rt△：半径、圆心到弦的垂线段、半弦·OABC3、两个定理：垂径定理、勾股定理小结小结运用垂径定理可以解决许多生产、生活实际问题，其中弓形是最常见的图形（如图），则弦a，弦心距d，弓形高h，半径r之间有以下关系：ABCDO2222adrd+h=r垂径定理的应用垂径定理的应用hrd2a(4)若，CD是直径,则、、.(1)若CDAB,CD⊥是直径,则、、.(2)若AM=MB,CD是直径,则、、.(3)若CDAB,AM=MB,⊥则、、.1.如图所示:口头练习●OABCD└MAM=BM⌒⌒AC=BC⌒⌒AD=BDCDAB⊥⌒⌒AC=BC⌒⌒AD=BDCD是直径⌒⌒AC=BC⌒⌒AD=BD⌒⌒AC=BCCDAB⊥AM=BM⌒⌒AD=BD2、判断下列说法的正误①平分弧的直径必平分弧所对的弦②平分弦的直线必垂直弦③垂直于弦的直径平分这条弦④平分弦的直径垂直于这条弦⑤弦的垂直平分线是圆的直径⑥平分弦所对的一条弧的直径必垂直这条弦⑦在圆中，如果一条直线经过圆心且平分弦，必平分此弦所对的弧⑧分别过弦的三等分点作弦的垂线，将弦所对的两条弧分别三等分1.过⊙o内一点M的最长的弦长为10㎝,最短弦长为8㎝,那么⊙o的半径是2.已知⊙o的弦AB=6㎝,直径CD=10㎝,且AB⊥CD,那么C到AB的距离等于3.已知⊙O的弦AB=4㎝,圆心O到AB的中点C的距离为1㎝,那么⊙O的半径为4.如图,在⊙O中弦AB⊥AC,OM⊥AB,ON⊥AC,垂足分别为M,N,且OM=2,0N=3,则AB=,AC=,OA=BAMCON5㎝1㎝或9㎝56413Cm1、如图，AB是⊙O的直径，CD为弦，CD⊥AB于E，则下列结论中不成立的是（）A、∠COE=∠DOEB、CE=DEC、OE=AED、BD=BC⌒⌒·OABECD2、如图，OE⊥AB于E，若⊙O的半径为10cm,OE=6cm,则AB=cm。·OABE解：连接OA，∵OE⊥AB∴cmOEOAAE86102222∴AB=2AE=16cm3、如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径。·OABE解：过点O作OE⊥AB于E，连接OA∴cmOEcmABAE3421∴cmOEAEAE5342222即⊙O的半径为5cm.4、如图，CD是⊙O的直径，弦AB⊥CD于E，CE=1，AB=10，求直径CD的长。·OABECD解：连接OA，∵CD是直径，OE⊥AB∴AE=1/2AB=5设OA=x，则OE=x-1，由勾股定理得x2=52+(x-1)2解得：x=13∴OA=13∴CD=2OA=26即直径CD的长为26.垂径定理的应用例1如图，一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.●OCDEF┗.)90(,mROFRm则设弯路的半径为,CDOE).(3006002121mCDCF得根据勾股定理,即,222OFCFOC.90300222RR.545,R得解这个方程.545m这段弯路的半径约为船能过拱桥吗?例2.如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？船能过拱桥吗解:如图,用表示桥拱,所在圆的圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与相交于点C.根据垂径定理,D是AB的中点,C是的中点,CD就是拱高.由题设得ABABABAB.5.121,4.2,2.7MNHNCDABABAD21,6.32.721DCOCOD.4.2R在RtOAD△中，由勾股定理，得,222ODADOA.)4.2(6.3222RR即解得R≈3.9（m）.在RtONH△中，由勾股定理，得,22HNONOH.6.35.19.322OH即.21.25.16.3DH∴此货船能顺利通过这座拱桥.达标检测一、填空1、已知AB、CD是⊙O中互相垂直的弦，并且AB把CD分成3cm和7cm的两部分，则圆心O和弦AB的距离为cm.2、已知⊙O的半径为10cm，弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为.3、已知⊙O中，弦AB=8cm，圆心到AB的距离为3cm，则此圆的半径为.4、在半径为25cm的⊙O中，弦AB=40cm，则此弦和弦所对的弧的中点的距离是.5、⊙O的直径AB=20cm,∠BAC=30°则弦AC=.14cm或2cm25cm10cm和40cm103cm