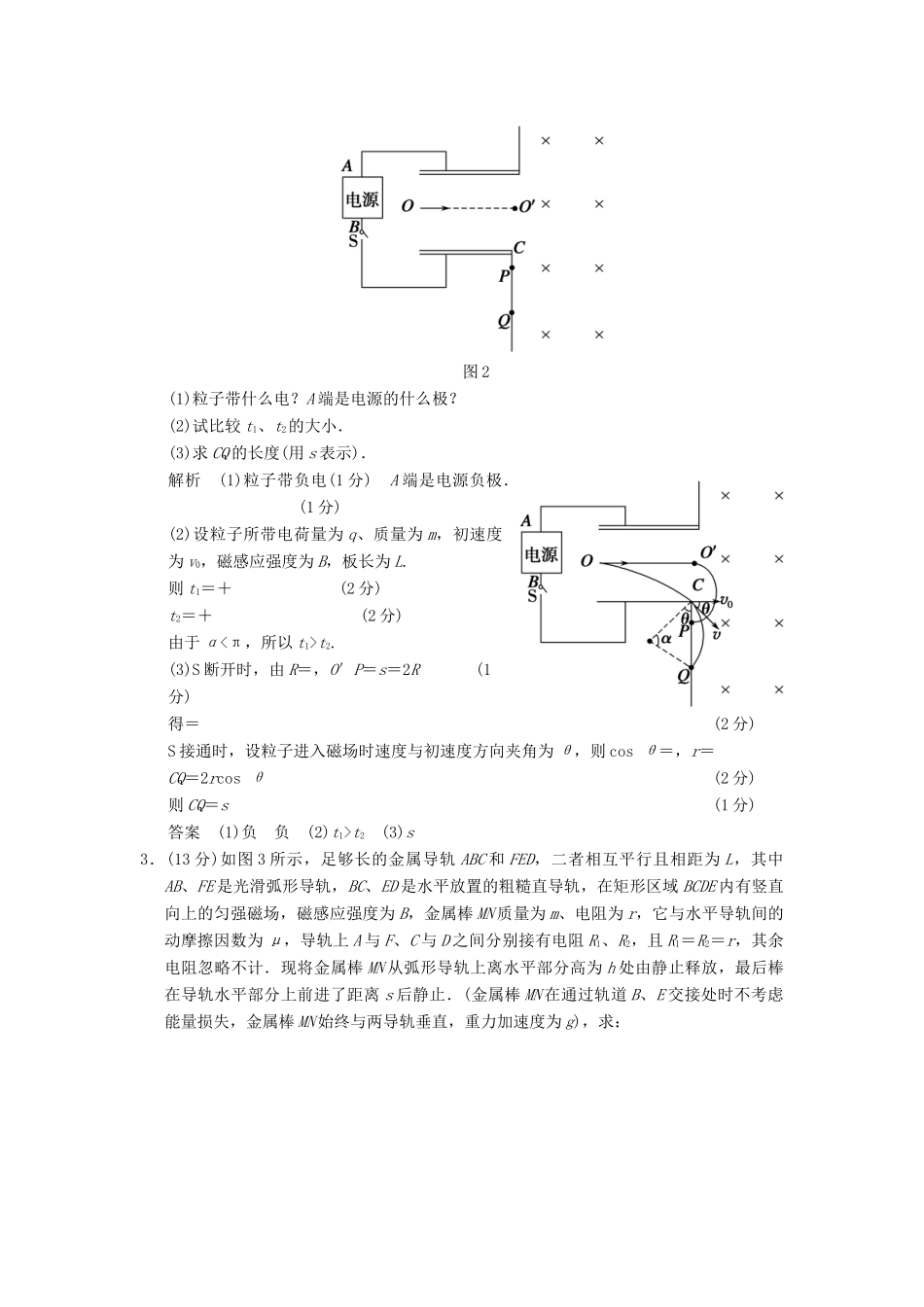
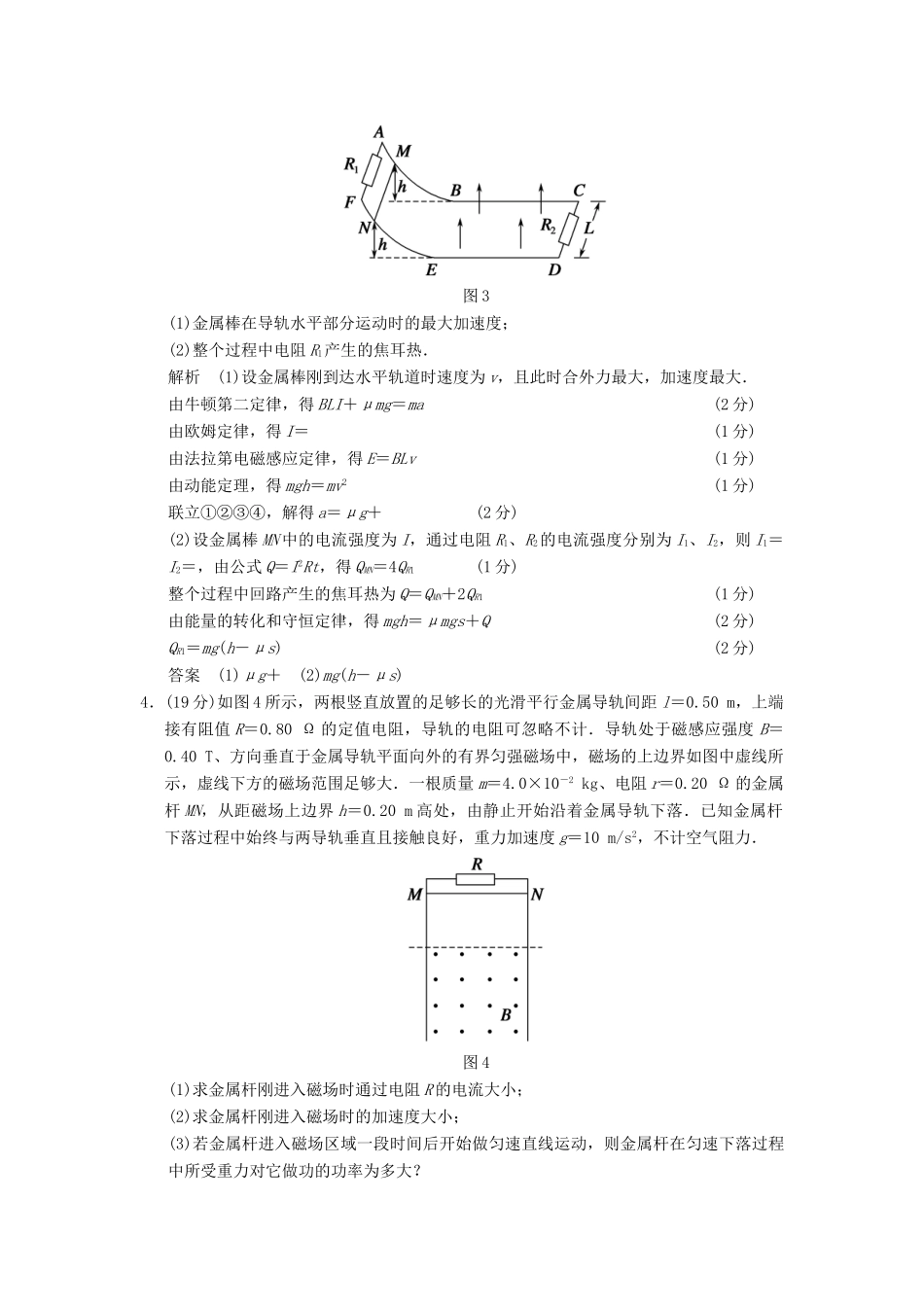
终极猜想十八电学综合(一)(本卷共4小题,满分58分.建议时间:45分钟)1.(13分)如图1所示,相距L=1m、电阻不计的平行光滑长金属导轨固定在绝缘水平面上,两导轨左端间接有阻值R=2Ω的电阻,导轨所在区域内加上与导轨所在平面垂直、方向相反的匀强磁场,磁场宽度d均为0.6m,磁感应强度大小B1=T、B2=0.8T.现有电阻r=1Ω的导体棒ab垂直导轨放置且接触良好,当导体棒ab从边界MN进入磁场后始终以速度5m/s作匀速运动,求:图1(1)棒ab在磁场B1中时克服安培力做功的功率;(2)棒ab经过任意一个磁场B2区域过程中通过电阻R的电量;(3)棒ab在磁场中匀速运动时电阻R两端电压的有效值.解析(1)在磁场B1中:E1=B1Lv,I1=(1分)FB=B1I1L(1分)P=FBv==W(2分)(2)在磁场B2中:E2=B2Lv(1分)I2=(1分)q=I2Δt2===0.16C.(2分)(3)设棒ab产生电动势的有效值为E.在磁场B1中产生的电动势为E1,磁场B2中产生的电动势为E2,回路在一个周期T内产生的焦耳热Q=×+×=×T(2分)解得:电动势的有效值为E=3V,(1分)电阻R两端电压的有效值为UR=R=2V.(2分)答案(1)W(2)0.16C(3)2V2.(13分)如图2所示,有一带电粒子(不计重力)从两块金属板正中间的O点沿轴线OO′射入,当开关S断开时,粒子射入匀强磁场中做匀速圆周运动,打在竖直挡板上的P点,测得O′P=s;当开关S接通时,粒子恰好从下极板端点C处射出,射出后打在竖直挡板的Q点.若用t1表示粒子从O到P的运动时间,用t2表示粒子从O到Q的运动时间.则:图2(1)粒子带什么电?A端是电源的什么极?(2)试比较t1、t2的大小.(3)求CQ的长度(用s表示).解析(1)粒子带负电(1分)A端是电源负极.(1分)(2)设粒子所带电荷量为q、质量为m,初速度为v0,磁感应强度为B,板长为L.则t1=+(2分)t2=+(2分)由于α<π,所以t1>t2.(1分)(3)S断开时,由R=,O′P=s=2R(1分)得=(2分)S接通时,设粒子进入磁场时速度与初速度方向夹角为θ,则cosθ=,r=CQ=2rcosθ(2分)则CQ=s(1分)答案(1)负负(2)t1>t2(3)s3.(13分)如图3所示,足够长的金属导轨ABC和FED,二者相互平行且相距为L,其中AB、FE是光滑弧形导轨,BC、ED是水平放置的粗糙直导轨,在矩形区域BCDE内有竖直向上的匀强磁场,磁感应强度为B,金属棒MN质量为m、电阻为r,它与水平导轨间的动摩擦因数为μ,导轨上A与F、C与D之间分别接有电阻R1、R2,且R1=R2=r,其余电阻忽略不计.现将金属棒MN从弧形导轨上离水平部分高为h处由静止释放,最后棒在导轨水平部分上前进了距离s后静止.(金属棒MN在通过轨道B、E交接处时不考虑能量损失,金属棒MN始终与两导轨垂直,重力加速度为g),求:图3(1)金属棒在导轨水平部分运动时的最大加速度;(2)整个过程中电阻R1产生的焦耳热.解析(1)设金属棒刚到达水平轨道时速度为v,且此时合外力最大,加速度最大.由牛顿第二定律,得BLI+μmg=ma(2分)由欧姆定律,得I=(1分)由法拉第电磁感应定律,得E=BLv(1分)由动能定理,得mgh=mv2(1分)联立①②③④,解得a=μg+(2分)(2)设金属棒MN中的电流强度为I,通过电阻R1、R2的电流强度分别为I1、I2,则I1=I2=,由公式Q=I2Rt,得QMN=4QR1(1分)整个过程中回路产生的焦耳热为Q=QMN+2QR1(1分)由能量的转化和守恒定律,得mgh=μmgs+Q(2分)QR1=mg(h-μs)(2分)答案(1)μg+(2)mg(h-μs)4.(19分)如图4所示,两根竖直放置的足够长的光滑平行金属导轨间距l=0.50m,上端接有阻值R=0.80Ω的定值电阻,导轨的电阻可忽略不计.导轨处于磁感应强度B=0.40T、方向垂直于金属导轨平面向外的有界匀强磁场中,磁场的上边界如图中虚线所示,虚线下方的磁场范围足够大.一根质量m=4.0×10-2kg、电阻r=0.20Ω的金属杆MN,从距磁场上边界h=0.20m高处,由静止开始沿着金属导轨下落.已知金属杆下落过程中始终与两导轨垂直且接触良好,重力加速度g=10m/s2,不计空气阻力.图4(1)求金属杆刚进入磁场时通过电阻R的电流大小;(2)求金属杆刚进入磁场时的加速度大小;(3)若金属杆进入磁场区域一段时间后开始做匀速直线运动,则金属杆在匀速下落过程中所受重力对它做功的功率为多大?解析(1)金属杆MN自由下落,设MN刚进入磁场时的速度为v,根据机...