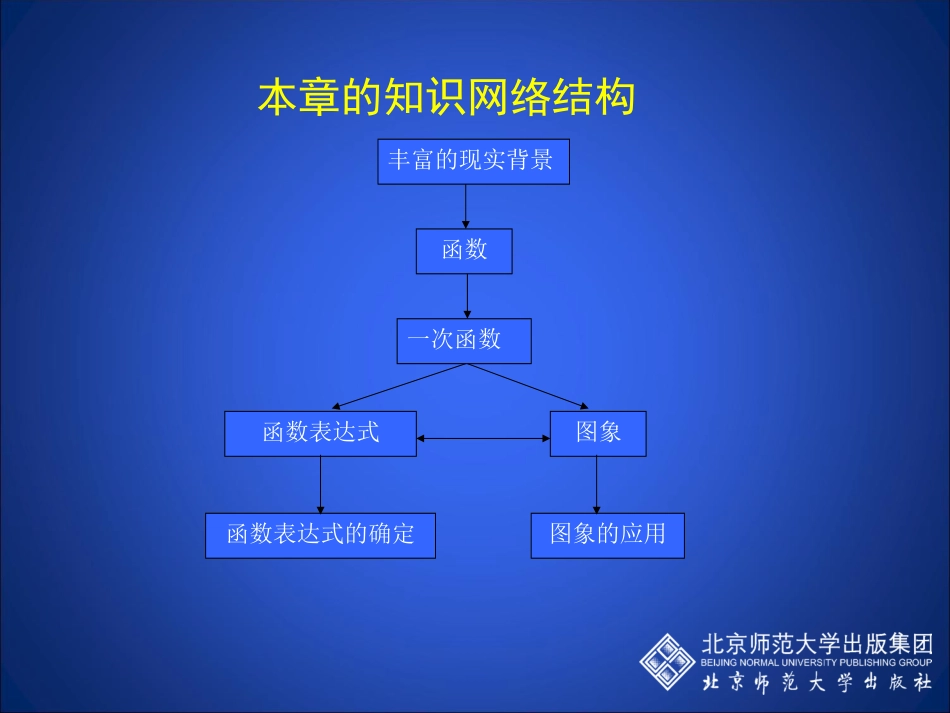
第四章一次函数回顾与思考自我复习成果展各小组派代表展示自己课前所归纳的本章重点内容与建立的知识结构图。并针对课本97页回顾与思考提出的五个问题中的一个问题进行成果汇报本章的知识网络结构丰富的现实背景函数一次函数函数表达式图象函数表达式的确定图象的应用•知识要点•(1)函数的概念。•(2)一次函数的概念•一次函数与正比例函数的关系。•(3)一次函数的不同表示方式。•(4)一次函数,正比例函数的图象各有什么特征。•①一次函数的图象是一条直线,经过点(0,b)和(,0),正比例函数的图象是经过原点的一条直线。•②在一次函数中,•当k>0时,y的值随着x值的增大而增大;•当k<0时,y的值随着x值的增大而减小。kb③直线的位置与k、b的关系:当k>0时,经过一、三象限;当k<0时,经过二、四象限当b>0时,经过一、二象限,当b<0时,经过三、四象限(5)确定一次函数表达式。(6)一次函数图象的应用。(7)两直线平行则K相等;两直线垂直则K互为负倒数;典型例题讲解•内容:例1、已知y是x的一次函数•(1)根据下表写出函数表达式;•(2)补全下表x134931y157(3)作出函数的图象,并回答下列问题。①随着x值的增加,y值的变化情况是________;②图象与图象与y的交点坐标有_______,与x轴的交点坐标是__________;③当x__________时,y≥0。•例2:甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离(千米)与(时间)之间的函数关系图像•(1)求甲从B地返回A地的过程中,与之间的函数关系式,并写出自变量的取值范围;•(2)若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?•解析:(1)由图象可知与之间是一次函数关系式,选择图象上两点代入即可;O31.5190x(时)y(千米)��•(2)将x=2代人到甲返回时距离和时间的关系中求出离开A地的距离,计算出乙的速度,从而算出时间.•解(1)设,根据题意得•解得••(2)当x=2时,∴骑摩托车的速度为(km/h)∴乙从A地到B地用时为(h)巩固练习•1、直线的图象经过的象限是()•A、第一、二、三象限•B、第一、二、四象限•C、第二、三、四象限•D、第一、三、四象限•2、时钟在正常运行时,分针每分钟转动6°,时针每分钟转动0.5°.在运行过程中,时针与分针的夹角会随时间的变化而变化.设时针与分针的夹角为y(度),运行时间为t(min),当时间从12:00开始到12:30止,y与t之间的函数图象是()By(度)�t(分)180OD30y(度)�t(分)195180OC30y(度)�t(分)180O3030AO165180t(分)y(度)�•【答案】A。•3、如图,一次函数=+的图象与轴的交点坐标为(2,0),则下列说法:•①随的增大而减小;•②>0;•③关于的方程+=0的解为=2.•其中说法正确的有(把你认为说法正确的序号都填上)xyy=kx+b2O4、如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,﹣2),求k与b的值。y=2xxyy=kx+bA(1,-2)O函数正比例函数一次函数解析式图象形状K>0K<0位置增减性位置增减性y=kx(k≠0)y=kx+b(k是常数,k≠0)过原点直线直线一三象限y随x的增大而增大b>0一、二、三象限y随x的增大而增大二四象限y随x的增大而减小y随x的增大而减小填表分析正比例函数和一次函数b<0一、三、四象限b>0一、二、四象限b<0二、三、四象限小结布置作业•课本99页6,7,8,9,14,18