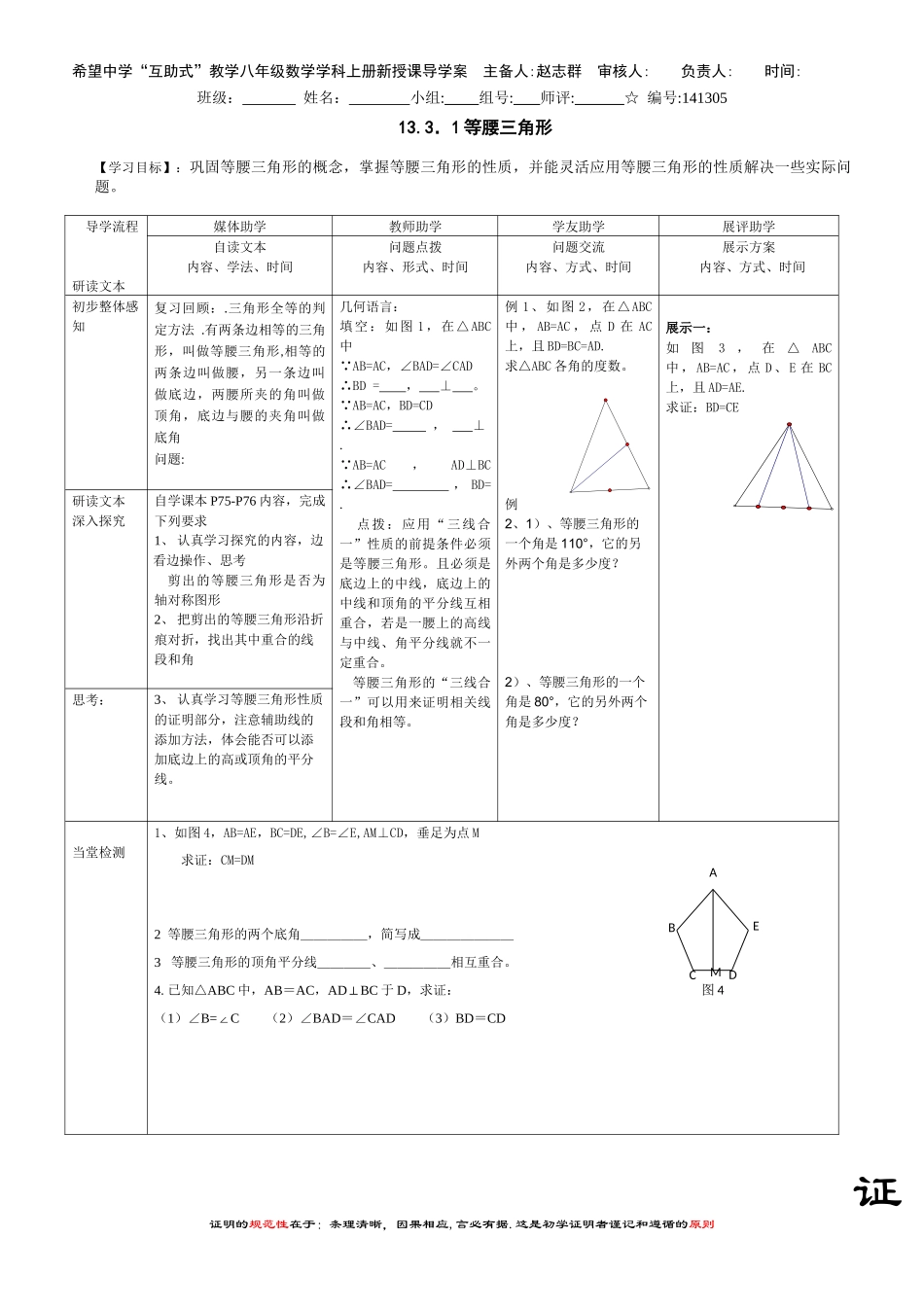
希望中学“互助式”教学八年级数学学科上册新授课导学案主备人:赵志群审核人:负责人:时间:班级:姓名:小组:组号:师评:☆编号:14130513.3.1等腰三角形【学习目标】:巩固等腰三角形的概念,掌握等腰三角形的性质,并能灵活应用等腰三角形的性质解决一些实际问题。导学流程研读文本媒体助学教师助学学友助学展评助学自读文本内容、学法、时间问题点拨内容、形式、时间问题交流内容、方式、时间展示方案内容、方式、时间初步整体感知复习回顾:.三角形全等的判定方法.有两条边相等的三角形,叫做等腰三角形,相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角问题:几何语言:填空:如图1,在△ABC中∵AB=AC,∠BAD=∠CAD∴BD=,⊥。∵AB=AC,BD=CD∴∠BAD=,⊥.∵AB=AC,AD⊥BC∴∠BAD=,BD=.点拨:应用“三线合一”性质的前提条件必须是等腰三角形。且必须是底边上的中线,底边上的中线和顶角的平分线互相重合,若是一腰上的高线与中线、角平分线就不一定重合。等腰三角形的“三线合一”可以用来证明相关线段和角相等。例1、如图2,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.求△ABC各角的度数。例2、1)、等腰三角形的一个角是110°,它的另外两个角是多少度?2)、等腰三角形的一个角是80°,它的另外两个角是多少度?展示一:如图3,在△ABC中,AB=AC,点D、E在BC上,且AD=AE.求证:BD=CE研读文本深入探究自学课本P75-P76内容,完成下列要求1、认真学习探究的内容,边看边操作、思考剪出的等腰三角形是否为轴对称图形2、把剪出的等腰三角形沿折痕对折,找出其中重合的线段和角思考:3、认真学习等腰三角形性质的证明部分,注意辅助线的添加方法,体会能否可以添加底边上的高或顶角的平分线。当堂检测1、如图4,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为点M求证:CM=DM2等腰三角形的两个底角_____,简写成_______3等腰三角形的顶角平分线____、_____相互重合。4.已知△ABC中,AB=AC,ADBC⊥于D,求证:(1)∠B=C∠(2)∠BAD=∠CAD(3)BD=CD证证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则图4EDCBAM