双曲线及其标准方程课件VIP免费

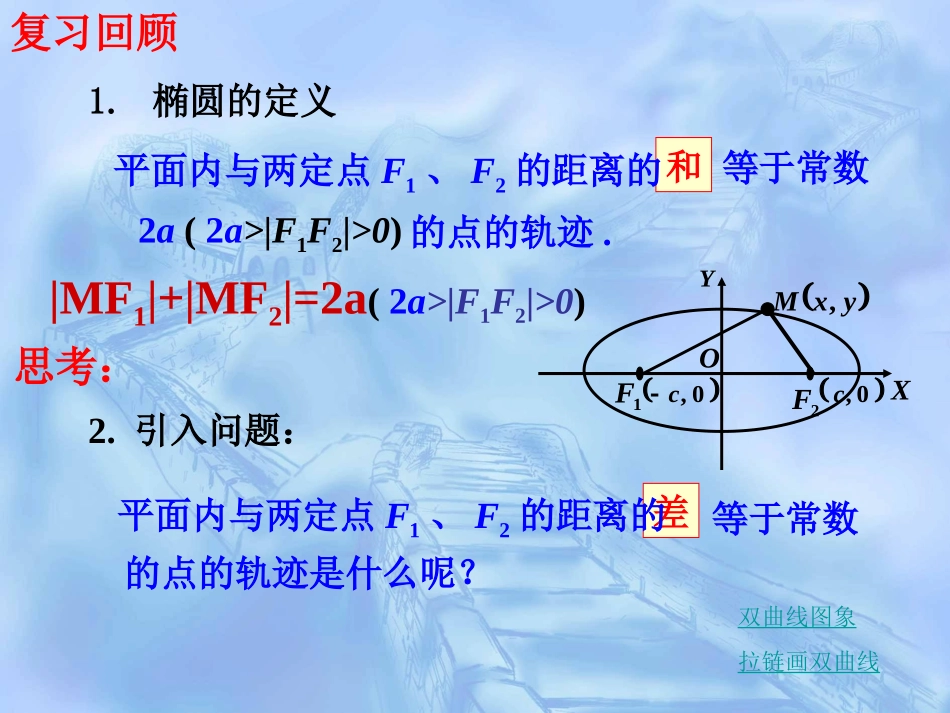
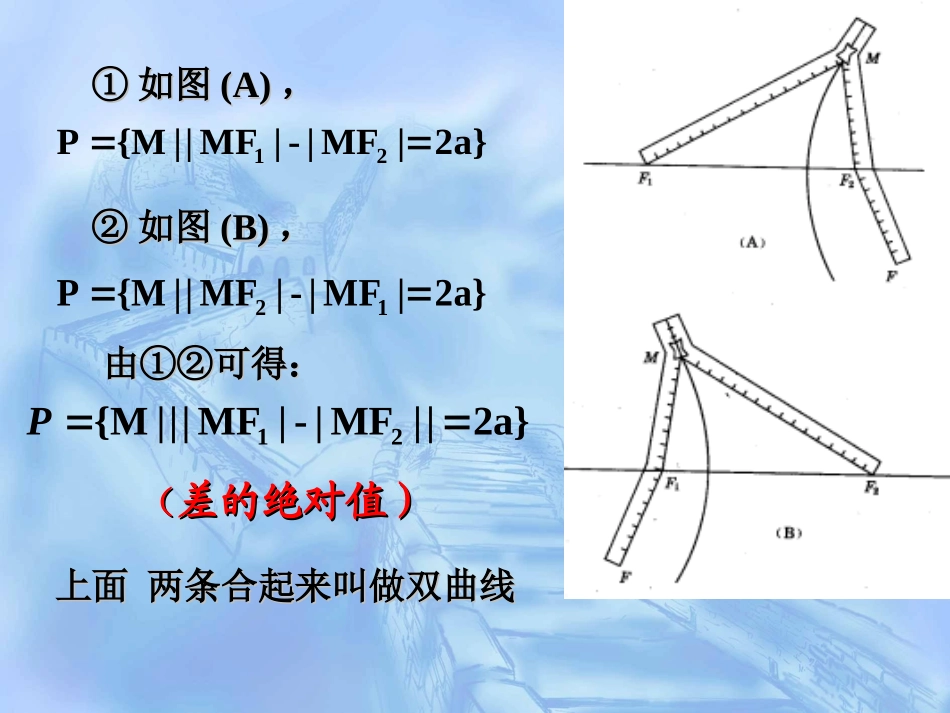
1.椭圆的定义和等于常数2a(2a>|F1F2|>0)的点的轨迹.平面内与两定点F1、F2的距离的1F2F0,c0,cXYOyxM,2.引入问题：差等于常数的点的轨迹是什么呢？平面内与两定点F1、F2的距离的复习回顾双曲线图象拉链画双曲线|MF1|+|MF2|=2a(2a>|F1F2|>0)思考：①①如图如图(A)(A)，，②②如图如图(B)(B)，，上面两条合起来叫做双曲线上面两条合起来叫做双曲线由①②可得：由①②可得：2a}|MF|-|MF||{MP212a}|MF|-|MF||{MP12（（差的绝对值）差的绝对值）2a}||MF|-|MF|||{M21P①两个定点F1、F2——双曲线的焦点;②|F1F2|=2c——焦距.0<2a<2c；平面内与两个定点F1，F2的距离的差的绝对值等于常数（小于︱F1F2︱)的点的轨迹叫做双曲线.一、双曲线定义（类比椭圆）思考：说明：||MF1|-|MF2||=2a(1)两条射线(2)不表示任何轨迹(3)(3)线段线段FF11FF22的垂直平分线的垂直平分线（3）若2a=0,则轨迹是什么？（1）若2a=2c,则轨迹是什么？（2）若2a>2c,则轨迹是什么？yoF2F1MxF2F1MxOy求曲线方程的步骤：二、双曲线的标准方程1.建系.以F1,F2所在的直线为x轴，线段F1F2的中点为原点建立直角坐标系2.设点．设M（x,y）,则F1(-c,0),F2(c,0)3.列式|MF1|-|MF2|=±2a4.化简aycxycx2)()(2222即aycxycx2)()(2222222222)(2)(ycxaycx222)(ycxaacx)()(22222222acayaxac222bac)0,0(12222babyax此即为焦点在x轴上的双曲线的标准方程12222byax12222bxayF2F1MxOyOMF2F1xy)00(ba，思考：若建系时,焦点在y轴上呢?看前的系数，哪一个为正，则在哪一个轴上22,yx22、双曲线的标准方程与椭圆的标准方程有何区、双曲线的标准方程与椭圆的标准方程有何区别与联系别与联系??11、如何判断双曲线的焦点在哪个轴上？、如何判断双曲线的焦点在哪个轴上？讨论：讨论：定义方程焦点a.b.c的关系F（±c，0）F（±c，0）a>0，b>0，但a不一定大于b，c2=a2+b2a>b>0，a2=b2+c2双曲线与椭圆之间的区别与联系双曲线与椭圆之间的区别与联系||MF1|－|MF2||=2a|MF1|+|MF2|=2a椭圆双曲线F（0，±c）F（0，±c）22221(0)xyabab22221(0)yxabab22221(0,0)xyabab22221(0,0)yxabab解：∴126PFPF∵焦点为12(5,0),(5,0)FF∴可设所求方程为:22221xyab(a>0,b>0).所以点P的轨迹方程为221916xy.∵1210FF>6,由双曲线的定义可知，点P的轨迹是一条双曲线,三、例题选讲0,5,0,521FF例1已知两定点,动点满足,求动点的轨迹方程PP126PFPF例1已知两定点,动点满足,求动点的轨迹方程126PFPF∵2a=6,2c=10,∴a=3,c=5.∴b2=52－32=16.例2、已知两地相距，在地听到炮弹爆炸声比在地晚，且声速为，求炮弹爆炸点的轨迹.BA、m800ABs2sm/340BA、BA、BA、B分析：依题意有，爆炸地点距两地的距离差值为一个定值，故而可知，爆炸点在以为焦点的双曲线上，又在地听到的晚，所以爆炸点离较远，应是靠近的一支。BA、BA、AA