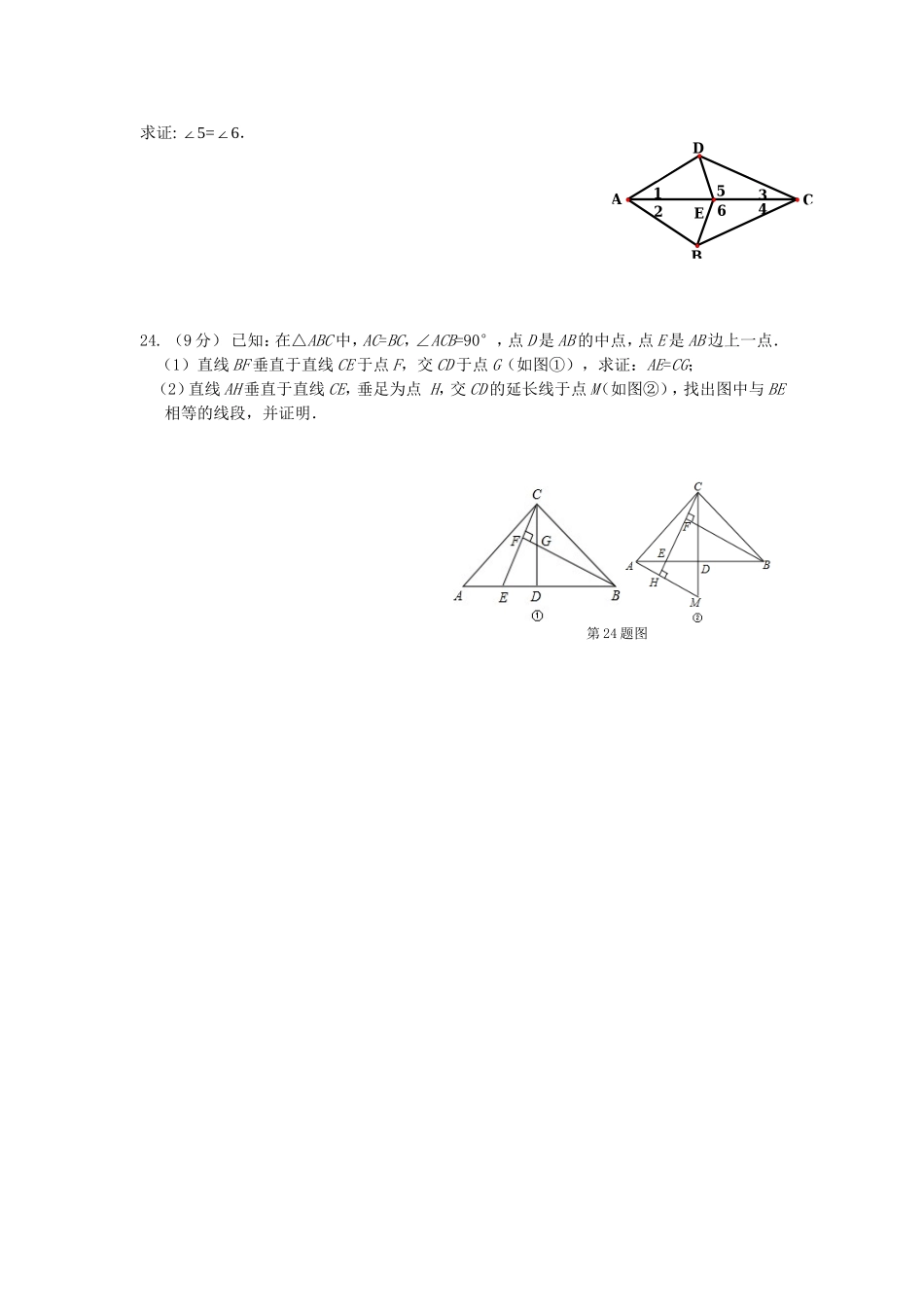
ADCB全等三角形小测班级:初二()班姓名:学号:评分:一、选择题(共5小题,每小题4分,共20分.)1.下列说法正确的是()A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等2.如图2,已知点P到AE,AD,BC的距离相等,则下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P是∠BAC,∠CBE,∠BCD的平分线的交点,其中正确的是().A.①②③④B.①②③C.④D.②③3.在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是().A.BC=B′C′B.∠A=∠A′C.AC=A′C′D.∠C=∠C′4.如图4,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由旋转,就做成了一个测量工件,则A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是().A.SASB.ASAC.SSSD.AAS5.如将一张长方形纸片按如图5的方式折叠,BC,BD为折痕,则∠CBD的度数为().A.60°B.75°C.90°D.95°二、填空题(共5小题,每小题4分,共20分)6.如图6,延长△ABC的中线AD到点E,使DE=AD,连接BE,EC,那么在四边形ABEC中共有__________对全等的三角形.7.如图7,△ABD≌△BAC,若AD=BC,则∠BAD的对应角为.8.如图8,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED=__________.9.如图9,AD=CB,若利用“边边边”来判定△ABC≌△CDA,则需添加一个直接条件是__________;若利用“边角边”来判定△ABC≌△CDA,则需添加一个直接条件是__________.10.如图10,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是5cm,则AB的长为__________.三、解答题(共5小题,共60分)11.(本题12分)已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.求证:(1)AF=CE;(2)AB∥CD.12.(本题12分)如图,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC.(1)图中有多少对全等三角形?请一一列举出来(不必说明理由);(2)求证:BE=CD图2图4图5图7图9图10图8图6图1313.(本题12分)已知BE⊥CD,BE=DE,BC=DA,求证:①△BEC≌△DAE;②DF⊥BC.14.(本题14分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.求证:(1)CF=EB.(2)AB=AF+2EB.15、(本题10分)如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_____个。请用尺规作图画出来。23.(10分)如图,在四边形ABCD中,E是AC上的一点,∠1=2∠,∠3=4∠,BCDEFA第14题图求证:5=6∠∠.24.(9分)已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.第24题图654321EDCBA参考答案1.B点拨:说法②③⑤正确.2.B点拨:甲图只有两个已知元素,不能确定与△ABC是否全等;乙图与△ABC满足SAS的条件,所以两图形全等;丙图与△ABC满足AAS的条件,所以两图形也全等.3.A4.C点拨:SSA不能作为全等的判定依据.5.A点拨:由题意得,OA=OA′,∠AOB=∠A′OB′,OB=OB′,所以全等的理由是边角边(SAS).6.C7.C8.B点拨:由题意,得∠ABC=∠EDC,CD=CB,∠ACB=∠ECD,所以三角形全等的理由是角边角(ASA).9.4点拨:由边角边可判定△BDE≌△CDA,△ADB≌△EDC,进而得BE=AC,AB=CE,再由边边边可判定△ABE≌△ECA,△ABC≌△ECB.10.50°点拨:根据三角形的内角和定理得∠C=50°,由全等三角形的性质得∠AED=∠C=50°.11.AB=CD∠CAD=∠ACB12.5点拨:如图,过点D作DE⊥AB于点E,由角的平分线的性质得DE=CD=2,所以△ABD的面积为12AB·DE=12×5×2=5.13.9<AB<19点拨:如图,由题意画出一个△ABC,延长AD至点E,使DE=AD,连接BE,则△BDE≌△CDA,得BE=AC=5,AE=14,在△ABE中,AE-BE...