周测1111VIP免费

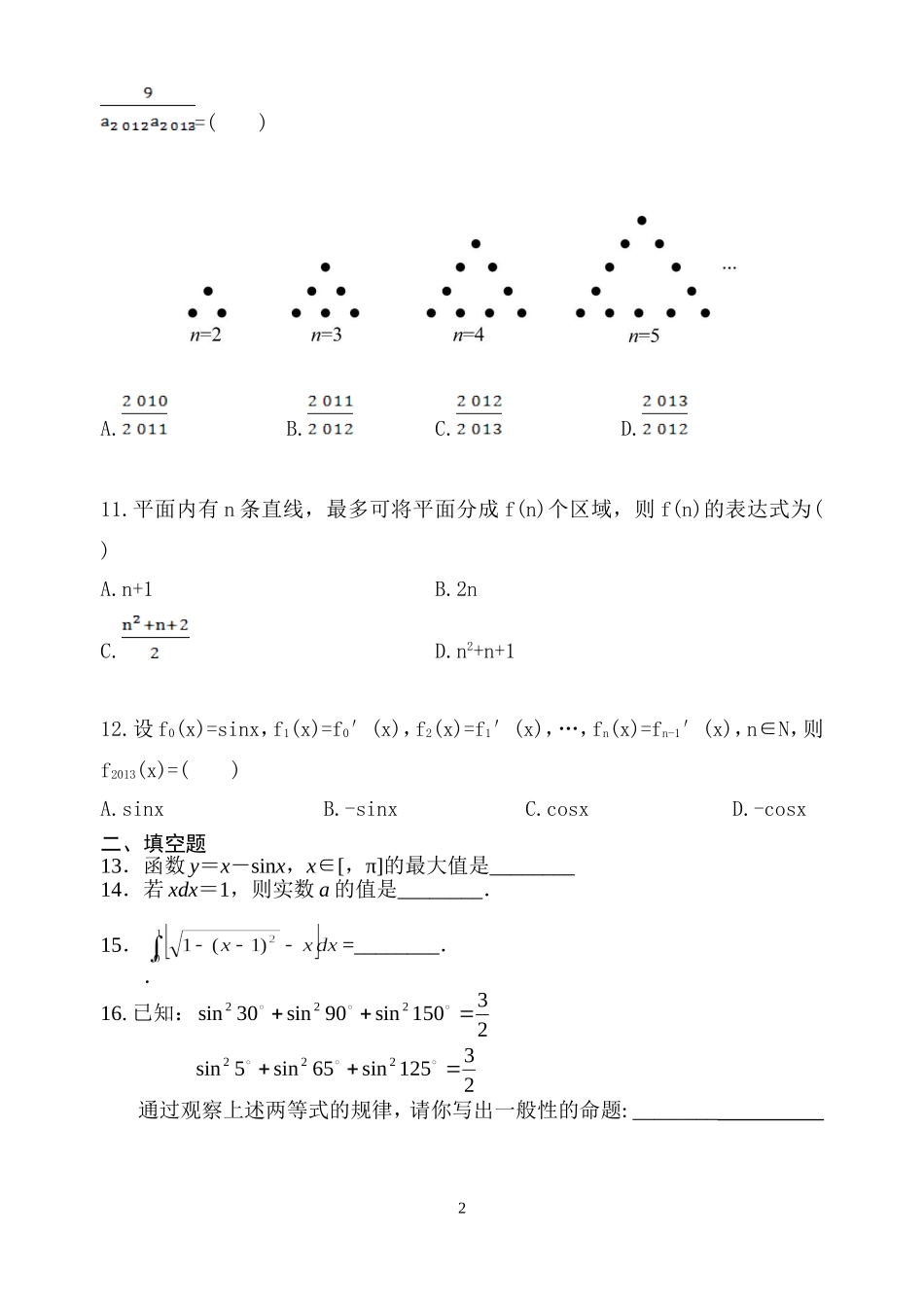
高二理科数学周测(4月6日)一、选择题1．函数f(x)＝x3－3x＋1在闭区间[－3,0]上的最大值、最小值分别是（）A．1，－1B．1，－17C．3，－17D．9，－192.函数的单调递增区间是（）A.B.C．D.3．已知f(x)＝x2＋2xf′(1)，则f′(0)等于（）A．0B．－4C．－2D．24.设函数f(x)＝2x＋－1(x＜0)，则f(x)（）A．有最大值B．有最小值C．是增函数D．是减函数5．曲线y＝2x－x3在横坐标为－1的点处的切线为l，则点P(3,2)到直线l的距离为()A.B.C.D.6．由直线x＝，x＝2，曲线y＝及x轴所围图形的面积是()A.B.C.ln2D．2ln27．已知直线y＝x＋1与曲线y＝lnx＋a相切，则a的值为()A．1B．2C．－1D．－28．数列2,5,11,20,,47,x…中的x等于（）A．28B．32C．33D．279.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案，则第n个图案中有白色地面砖的块数是()A.4n+2B.4n-2C.2n+4D.3n+310.如图所示，将若干个点摆成三角形图案，每条边(包括两个端点)有n(n>1，n∈N*)个点，相应的图案中总的点数记为an，则+++…+1=()A.B.C.D.11.平面内有n条直线，最多可将平面分成f(n)个区域，则f(n)的表达式为()A.n+1B.2nC.D.n2+n+112.设f0(x)=sinx，f1(x)=f0′(x)，f2(x)=f1′(x)，…，fn(x)=fn-1′(x)，n∈N，则f2013(x)=()A.sinxB.-sinxC.cosxD.-cosx二、填空题13．函数y＝x－sinx，x∈[，π]的最大值是________14．若xdx＝1，则实数a的值是________．15．=________．．16.已知：23150sin90sin30sin22223125sin65sin5sin222通过观察上述两等式的规律，请你写出一般性的命题:________2班别：________姓名：________成绩：________一、选择题123456789101112二、填空题13.________14.________15.________16.________三、解答题17.已知n≥0，试用分析法证明：-<-.18.已知cbxaxxf24)(的图象经过点(0,1)，且在1x处的切线方程是2yx（1）求)(xfy的解析式；（2）求)(xfy的单调递增区间。319.在数列中，a1=1，a2=，且an+1=.(1)求a3，a4，猜想an的表达式，并加以证明.(2)设bn=，求证：对任意的n∈N*，都有b1+b2+…+bn<.4周测答案(4月6日)123456789101112CABAADBBABCC13.14.15.16.2223sin(60)sinsin(60)217.【证明】要证上式成立，需证+<2.需证(+)2<(2)2，需证n+1>，需证(n+1)2>n2+2n，需证n2+2n+1>n2+2n，只需证1>0.因为1>0显然成立，所以原命题成立.18.解：（1）cbxaxxf24)(的图象经过点(0,1)，则1c，'3'()42,(1)421,fxaxbxkfab切点为(1,1)，则cbxaxxf24)(的图象经过点(1,1)得591,,22abcab得4259()122fxxx（2）'3310310()1090,0,1010fxxxxx或单调递增区间为310310(,0),(,)1010519.【解析】(1)容易求得：a3=，a4=.故可以猜想an=，n∈N*.下面利用数学归纳法加以证明：(i)显然当n=1，2，3，4时，结论成立，(ii)假设当n=k(k≥4，k∈N*)时，结论也成立，即ak=.那么当n=k+1时，由题设与归纳假设可知：ak+1======.即当n=k+1时，结论也成立，综上，对任意n∈N*，an=成立.(2)bn====(-)，所以b1+b2+…+bn=[(-1)+(-)+(-)+…+(-)]=(-1)，6所以只需要证明(-1)<⇔<+1⇔3n+1<3n+2+1⇔0<2(显然成立)，所以对任意的n∈N*，都有b1+b2+…+bn<.7