相似三角形复习课件VIP免费

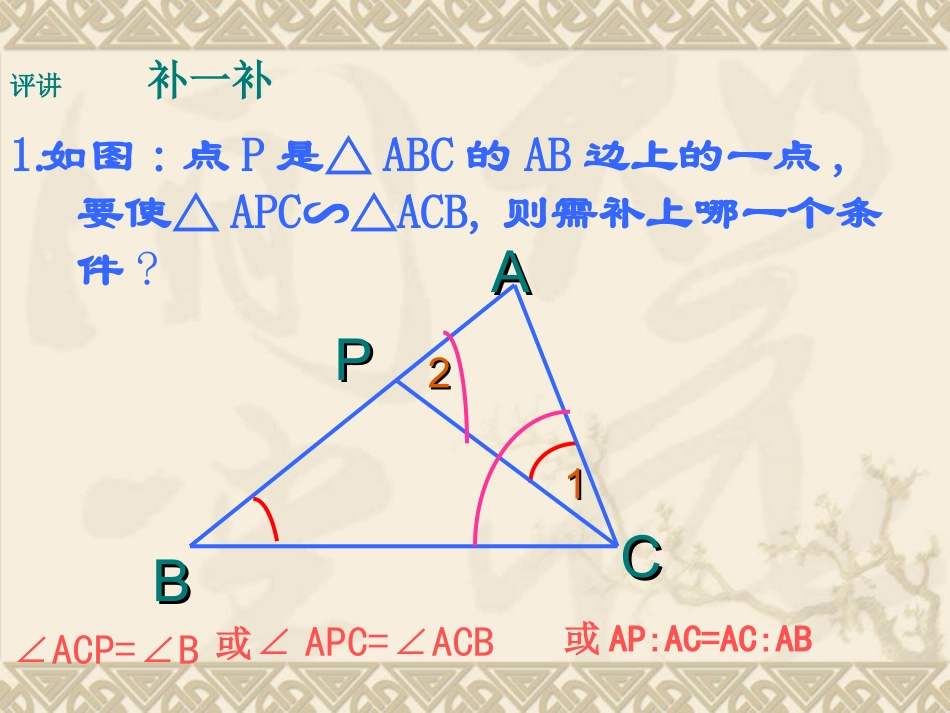
2010-03-20（二）如图:点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?11∠ACP=∠BAACCBBPP22或∠APC=∠ACB或AP:AC=AC:AB评讲补一补1.2.在□ABCD中,AE:BE=1:2.ABCDEF算一算若SAEF△=6cm2,则S△CDF=cm254S△ADF=____cm2183.已知三角形甲三边的比为3:4:6，和它相似的三角形乙的最大边为10cm，则三角形乙的最短边为______cm.DEFABC解:设三角形甲为△ABC，三角形乙为△DEF，且△DEF的最大边为DE，最短边为EF △DEF∽△ABC∴DE:EF=6:3即10:EF=6:3∴EF=5cm三角形相似的判定方法有哪几种?美好回忆知识回顾1、平行定理ABCDEDEABC DEBC,∥ADEABC∴△∽△三角形相似的判定方法有哪几种?1、平行定理2、两个角对应相等的两个三角形相似A=DB=E△ABC∽△DEFAABBCCDDEEFF3、两边对应成比例且夹角相等的两个三角形相似.三角形相似的判定方法有哪几种?1、平行定理2、两个角对应相等的两个三角形相似ABDE=ACDFA=D△ABCDEF∽△AABBCCDDEEFF3、两边对应成比例且夹角相等的两个三角形相似.三角形相似的判定方法有哪几种?1、平行定理2、两个角对应相等的两个三角形相似4、三边对应成比例的两个三角形相似.AABBCCDDEEFFABDE=ACDF=BCEF△ABCDEF∽△相似三角形的性质有哪些？1、相似三角形的对应角相等，对应边成比例2、相似三角形的周长比等于相似比，对应高（中线、角平分线）的比等于相似比3、相似三角形的面积比等于相似比的平方准备如图，AB⊥BC,DC⊥BC,AE⊥ED，B、E、C在一条直线上求证：ΔABE∽ΔECD证明： ∠AEB+∠AED+∠DEC=180°∠AED=90°∴∠AEB+∠DEC=90° 在直角三角形ABE中，∠AEB+∠A=90°∴∠A=∠DEC又 ∠B=∠C=90°∴ΔABE∽ΔECDAABBCCDDEEAABBAABB例1、如图，已知：ABDB⊥于点B，CDDB⊥于点D，AB=6，CD=4，BD=14.问：在DB上一动点P，在DB上是否存在P点，使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似？如果存在，计算出点P的位置；如果不存在，请说明理由。4614ADCB例1、如图，已知：ABDB⊥于点B，CDDB⊥于点D，AB=6，CD=4，BD=14.问：在DB上一动点P，在DB上是否存在P点，使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似？如果存在，计算出点P的位置；如果不存在，请说明理由。例:解（1）存在这样的点P，使△ABP∽△CDP设PD=x，则PB=14―x，∴6：4=（14―x）:x则有AB:CD=PB:PD∴x=5.6P6x14―x4ADCBP（2）存在这样的点P,使△ABPPDC,∽△则则有AB:PD=PB:CD设PD=x，则PB=14―x，∴6：x=（14―x）:4∴x=2或x=12∴x=2或x=12或x=5.6时，以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似46x14―xDBCAp二次函数y=x的图像如图所示，过y轴上一点E（0，2）的直线与抛物线交于A、B两点，过点A、B分别作y轴的垂线，垂足分别为C、D.（1）当点A的横坐标为（-2，0.5）时，求点B的坐标（2）在（1）的情况下，分别过点A、B作AF⊥X轴于F，BG⊥X轴于G，在FG上是否存在点P，使∠APB为直角，若存在，求点P的坐标；若不存在，请说明理由;812例2解答题xyOADCEB812x)2x5.12812x∴=∴=解 A（-2，0.5），E（0，2）∴AC=2，EC=2-0.5=1.5设点B的横坐标为x，而点B在抛物线上 AC⊥y轴，BD⊥y轴∴BD∥AC∴ΔACE∽ΔBDE解得x=8，x=-2（舍去）∴B（8，8）5.12812x∴=∴B(x,∴BD=x,DE=DO-EO=x-2812yxOADCEBPGFxOADCEBPFG四、回顾和小结1、相似三角形的判定、性质与方程与运动、函数等的综合应用，这是中考当中常见的方向，特别注意与运动相结合。同学们一定要注重分析题的方法，总结经验。2、要细心，分析问题清楚、全面，不能有疏漏。14说一说证明: 四边形ABCD是正方形ABCDEF1234、如图,正方形ABCD中,E是DC中点,FC=BC.求证:AE⊥EF∴BC=CD=AD，∠D=C=90°∠ E是DC中点，FC=BC14∴FC:CE=1:2∴△ADE∽ECF△∴∠1=2∠ ∠D=90°∴∠1+3=90°∠∴∠2+3=90°∠∴AEEF⊥DE:AD=1:2在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4x4的格纸中,△ABC是一个格点三角形AABBCC创新应用画一画AABBCCAABBCC(1)在图1中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)(2)在图2中,请你再画一个格点三角形,使它与△ABC相似(...