分式的基本性质（2）VIP免费

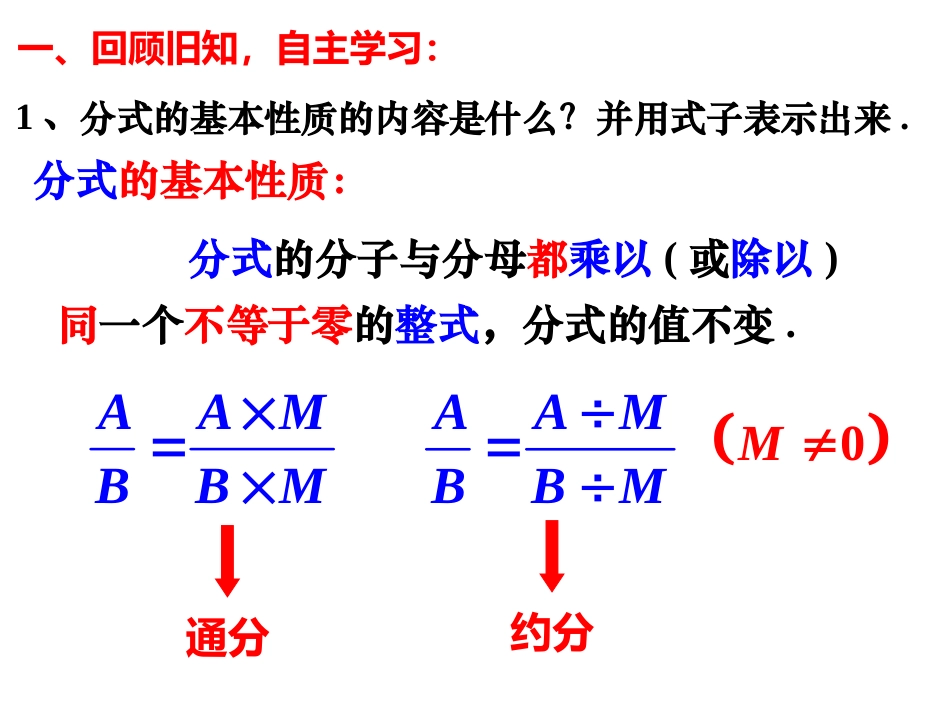
分式的分子与分母都乘以(或除以)同一个不等于零的整式，分式的值不变.分式的基本性质：AAMBBMAAMBBM0M一、回顾旧知，自主学习：通分约分1、分式的基本性质的内容是什么？并用式子表示出来.2、下列分式从左到右的变形是否正确？2221(1)(1)1(1)(1)1xxxxxxx①222(1)(1)1(1)(1)11xxxxxxx②本题中隐含了x≠-1.不一定正确.正确.只有当x≠-1时上述变形才正确.3、分式约分的基本方法如何？①找出分子与分母的公因式，约去公因式；②若分子或分母是多项式，则往往要先把分子、分母进行因式分解，然后再进行约分.要求：约分后，分子与分母不再有公因式（要彻底），所得分式为最简分式.22222169159xaxxaxxx①②③4、约分：2=5x=1a3=3xx通分：分的通分：数式把几个异分母的分化为同分母的分，而不改变分的值.数式式数数式最简公分母：各分母所有因式的最高次幂的积.分式通分的意义：将异分母分式化为同分母分式，应用于异分母分式的加减运算等.二、边学边导，基础过关：求下列各组分式的最简公分母并通分：2211abab①，；222134ababc②，；11xyxy③，；22211.xyxxy④；最简公分母：通分：22ab222211ababbabbb==222211ababaaaba==最简公分母：通分：2212abc2222482233412ababacbacacac==2222311443312abcabbbabcbc==最简公分母：通分：22xy22()()11()xyxyxyxxxyyy==最简公分母：通分：32xxy32222211()xyxxxxyxxy==22()()11()xyxyxyxxxyyy==2322()()11()xxyxxxyxxxxyyyy==()()xxyxy分式通分小结：一、依据：通分也是应用分式的基本性质把分式的分子、分母都乘以同一个整式，使分式的值不变.二、关键：确定最简公分母.三、求几个分式的最简公分母的方法与步骤：1、系数：；2、字母或因式：；3、指数：；4、积：.把几个异分母的分式分别化为与原来的分式值相等的同分母的分式叫分式通分.各分母系数的最小公倍数各分母所有的字母或因式各分母所有的字母或因式的最高次数各分母所有因式的最高次幂的积（包括与系数的积）三、精讲点拨，巩固提升：求下列各组分式的最简公分母并通分：四、达标检测，当堂过关：求下列各组分式的最简公分母并通分：最简公分母：最简公分母：最简公分母：2218abc3(1)x(1)(1)xxx22223168363xaxabaaccbacxabc22222991228yyabcabcbbyabcb2322(2)(1)(1)(1)(1(2)(1)())1xxxxxxxxx3323(1)23(1)xxxx2232(1)(1)5515((1)1)(1)xxxxxx332(1)xx2(1)(11(11(1)(1)1))xxxxxxxxxx2(1)(11(11(1)(1)1))xxxxxxxxxx221(1)(1()(1))1xxxxxxxxxxx一、依据：通分也是应用分式的基本性质把分式的分子、分母都乘以同一个整式，使分式的值不变.二、关键：确定最简公分母.三、求几个分式的最简公分母的方法与步骤：1、系数：；2、字母或因式：；3、指数：；4、积：.把几个异分母的分式分别化为与原来的分式值相等的同分母的分式叫分式通分.各分母系数的最小公倍数各分母所有的字母或因式各分母所有的字母或因式的最高次数各分母所有因式的最高次幂的积（包括与系数的积）小结：五、拓展延伸，智力闯关：34提示：113ab3baab3abab整体代入求解.2322(()3)aabbababaabbabab又