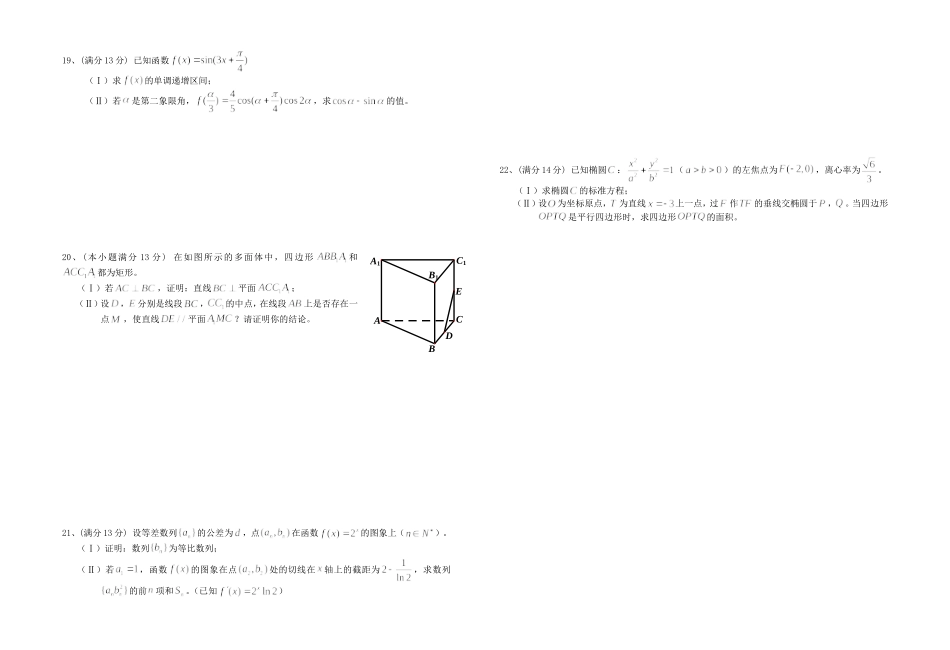
龙泉中学高二下学期数学(文)周练1班级姓名成绩一、选择题(每小题5分,共50分)1、已知集合,集合为整数集,则()A、B、C、D、2、在“世界读书日”前夕,为了了解某地名居民某天的阅读时间,从中抽取了名居民的阅读时间进行统计分析。在这个问题中,名居民的阅读时间的全体是()A、总体B、个体C、样本的容量D、从总体中抽取的一个样本3、为了得到函数的图象,只需把函数的图象上所有的点()A、向左平行移动个单位长度B、向右平行移动个单位长度C、向左平行移动个单位长度D、向右平行移动个单位长度4、某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是()(锥体体积公式:,其中为底面面积,为高)A、B、C、D、5、若,,则一定有()A、B、C、D、6、执行如图的程序框图,如果输入的,那么输出的的最大值为()A、B、C、D、7、已知,,,,则下列等式一定成立的是()A、B、C、D、8、如图,从气球上测得正前方的河流的两岸,的俯角分别为,,此时气球的高是,则河流的宽度等于()A、B、C、D、9、设,过定点的动直线和过定点的动直线交于点,则的取值范围是()A、B、C、D、10、已知为抛物线的焦点,点,在该抛物线上且位于轴的两侧,(其中为坐标原点),则与面积之和的最小值是()A、B、C、D、题号12345678910答案二、填空题(请把答案填在题中横线上,每小题5分,共35分)11、___________.12、双曲线的离心率等于____________.13、复数____________.14、设是定义在上的周期为的函数,当时,,则____________.15、平面向量,,(),且与的夹角等于与的夹角,则____________.16、.17、命题“存在”的否定是_________________________________.三、解答题(解答应写出必要的文字说明、证明过程或演算步骤)18、(满分12分)一个盒子里装有三张卡片,分别标记有数字,,,这三张卡片除标记的数字外完全相同。随机有放回地抽取次,每次抽取张,将抽取的卡片上的数字依次记为,,。(Ⅰ)求“抽取的卡片上的数字满足”的概率;(Ⅱ)求“抽取的卡片上的数字,,不完全相同”的概率。侧视图俯视图1122221130°75°60mCBA19、(满分13分)已知函数(Ⅰ)求的单调递增区间;(Ⅱ)若是第二象限角,,求的值。20、(本小题满分13分)在如图所示的多面体中,四边形和都为矩形。(Ⅰ)若,证明:直线平面;(Ⅱ)设,分别是线段,的中点,在线段上是否存在一点,使直线平面?请证明你的结论。21、(满分13分)设等差数列的公差为,点在函数的图象上()。(Ⅰ)证明:数列为等比数列;(Ⅱ)若,函数的图象在点处的切线在轴上的截距为,求数列的前项和。(已知)22、(满分14分)已知椭圆:()的左焦点为,离心率为。(Ⅰ)求椭圆的标准方程;(Ⅱ)设为坐标原点,为直线上一点,过作的垂线交椭圆于,。当四边形是平行四边形时,求四边形的面积。DEB1C1ACBA1龙泉中学高二数学下文周练1参考答案一、选择题题号12345678910答案DAADBCBCBB11.12.13.14.115.216.16.17.对任意的18.本题主要考察随机事件的概率、古典概型等概念及相关计算,考察应用意识。解:(Ⅰ)由题意,所有的可能为:(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),(3,3,1),(3,3,2),(3,3,3),共27种.设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种,所以P(A)==.因此,“抽取的卡片上的数字满足a+b=c”的概率为.(Ⅱ)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,则事件包括(1,1,1),(2,2,2),(3,3,3),共3种.所以因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为19.本题主要考查正弦型函数的性质,二倍角与和差角公式,简单的三角恒等变换等基础知识,考查运算求解能力,考查分类与整合、化归与转化等数学思想。解:(Ⅰ)因为函数的单调递增区间为由-+2kπ≤3x+≤+2kπ,k∈Z,得-+≤x≤+...