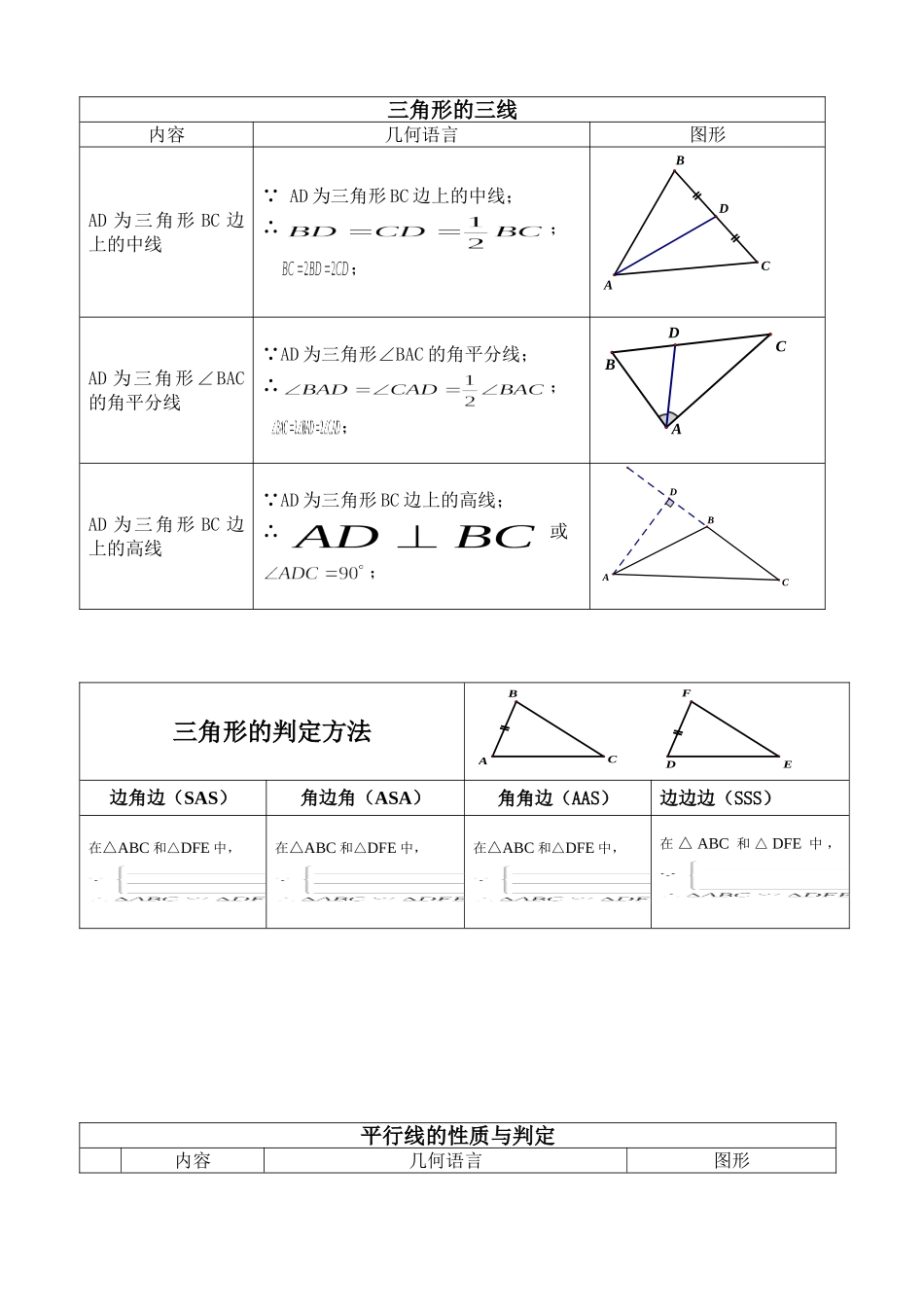
常用几何语言汇总依据内容几何语言图形常理线段总长度等于各个线段之和AD=AB+BC+CD.CADB大角等于大角里面各个角之和∠AOC=∠AOB+∠BOC;或∠AOC=∠1+∠2.21AOBC等式的基本性质已知:AB=CD,得到AC=BD∵AB=CD;∴AB+BC=CD+BC(等式的性质)即AC=BD.CADB已知:AC=BD,得到AB=CD∵AC=BD;∴AC-BC=BD-BC(等式的性质)即AB=CD.已知:∠1=∠3,得到∠AOC=∠DOB∵∠1=∠3;∴∠1+∠2=∠3+∠2(等式的性质)即∠AOC=∠DOB.321AOBCD已知:∠AOC=∠DOB,得到∠1=∠3∵∠AOC=∠DOB;∴∠AOC-∠2=∠DOB-∠2(等式的性质)即∠1=∠3.同角的余角相等已知,CD⊥AB,AC⊥BC;得到∠A=∠2,∠B=∠1;∵CD⊥AB,AC⊥BC;∴∠AOC=∠DOB=90°.(垂直定义)∵∠B+∠2=90°,∠A+∠B=90°;(直角三角形的两个锐角互余)∴∠A=∠2.(同角的余角相等)或(等量代换)12DCBA同角的补角相等已知∠1=∠2;得到∠ACB=∠ACD;∵∠1=∠2;又∠ACB+∠1=180°;∠ACD+∠2=180°(平角定义)∴∠ACB=∠ACD(同角的补角相等)21DACB三角形的三线内容几何语言图形AD为三角形BC边上的中线∵AD为三角形BC边上的中线;∴;;DABCAD为三角形∠BAC的角平分线∵AD为三角形∠BAC的角平分线;∴;;DACBAD为三角形BC边上的高线∵AD为三角形BC边上的高线;∴或;DBAC三角形的判定方法EDFBAC边角边(SAS)角边角(ASA)角角边(AAS)边边边(SSS)在△ABC和△DFE中,在△ABC和△DFE中,在△ABC和△DFE中,在△ABC和△DFE中,平行线的性质与判定内容几何语言图形性质两直线平行,同位角相等.∵AB∥CD;∴HGBADEFC两直线平行,内错角相等.∵AB∥CD;∴两直线平行,同旁内角互补.∵AB∥CD;∴判定同位角相等,两直线平行.∵∴AB∥CD.(同位角相等,两直线平行)内错角相等,两直线平行.∵∴AB∥CD.(内错角相等,两直线平行)同旁内角互补,两直线平行.∵∴AB∥CD.(同旁内角相等,两直线平行)