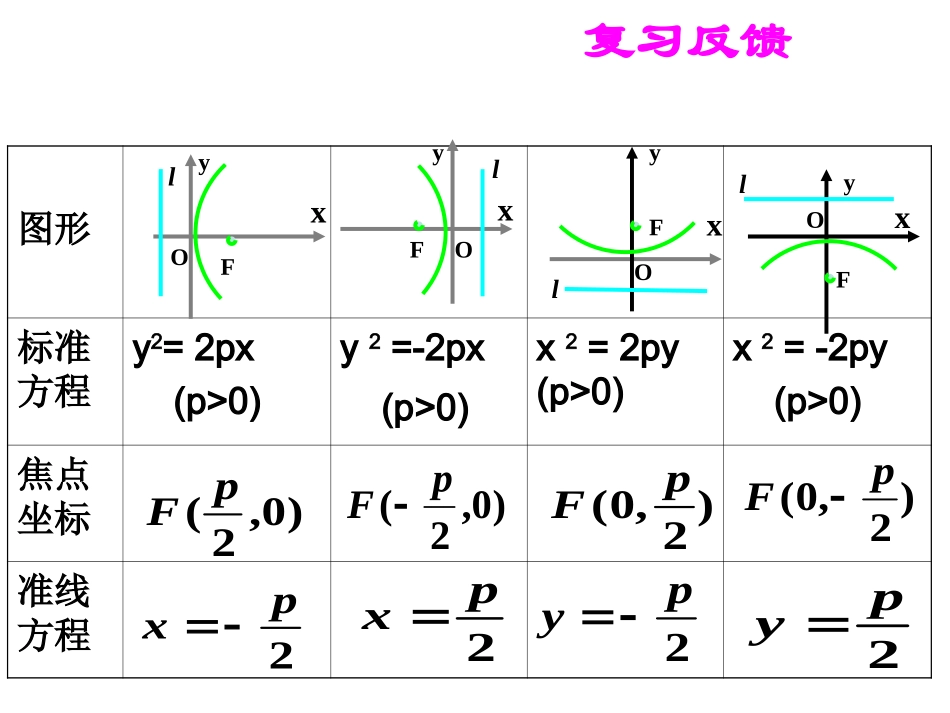
复习反馈图形标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)焦点坐标准线方程OlFxyOlFxyOlFxyOlFxy)0,2(pF)0,2(pF)2,0(pF)2,0(pF2px2px2py2py1111离心率e(0,0)(0,0)(0,0)顶点y轴y轴x轴x轴对称轴y≤0,xR∈y≥0,xR∈x≤0,yR∈x≥0,yR∈范围图形x2=-2pyx2=2pyy2=-2pxy2=2px标准方程lOFxy请同学们仿照研究椭圆的性质的方法研究抛物线的性质(0,0)lOFxyOlFxyyOlFx小结:抛物线只有:一个焦点,一个顶点,一条准线,一条对称轴,没有中心。(1)一次项的变量为x(或y),则x(或y)轴为抛物线的对称轴。反之亦然。(2)一次项的符号决定开口方向。(3)由已知条件求抛物线的标准方程时,首先要确定类型,再求出方程中的焦参数P--焦点到准线的距离。说明:例1、已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M,求它的标准方程,并用描点法画出图形。)22,2(y2=4x例3、斜率为1的直线l经过y2=4x的焦点,且与抛物线相交于A、B两点,求线段AB的长。XYOFAlA’B’B解法2:解法1:例4、已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k,当k为何值时,直线l与抛物线:1、只有一个交点;2有两个交点;3没有交点。注意:1、对k取值进行讨论;2、k对交点个数的影响,主要是运用二次方程的判别式⊿。例5、由点(-2,0)向抛物线y2=4x引弦,求弦中点的轨迹方程.y2=2(x+2),(x>2)小结:三动点问题----用消去法。反馈练习1、抛物线的顶点在坐标原点,对称轴是y轴,且顶点和焦点之间的距离为2,则该抛物线的方程是()Ax2=4yBx2=-4yCx2=±4yDx2=±8y2、下列关于抛物线的条件中,能确定抛物线的方程是标准方程的是()A顶点在原点B对称轴是坐标轴C焦点是(0,a),准线方程是x=-a(a≠0)D顶点在原点,准线方程式y=a(a≠0)3、顶点在原点,对称轴是坐标轴,且经过点M(1,-1)的抛物线方程是()Ay2=xBy2=-xCy2=x,x2=-yDX2=-YDDC4、等腰直角三角形ABO的三个顶点都在抛物线y2=2px,(p>0)上,且O是直角顶点,则|AB|=_______5、抛物线上的一点A(m,-3)到准线的距离为5,则A到顶点的距离为________4P33课后小结抛物线的标准方程的形式比较多,它们的几何性质要牢记,应用时应注意抛物线焦点位置。根据性质求抛物线方程时,一般是采用待定系数法。