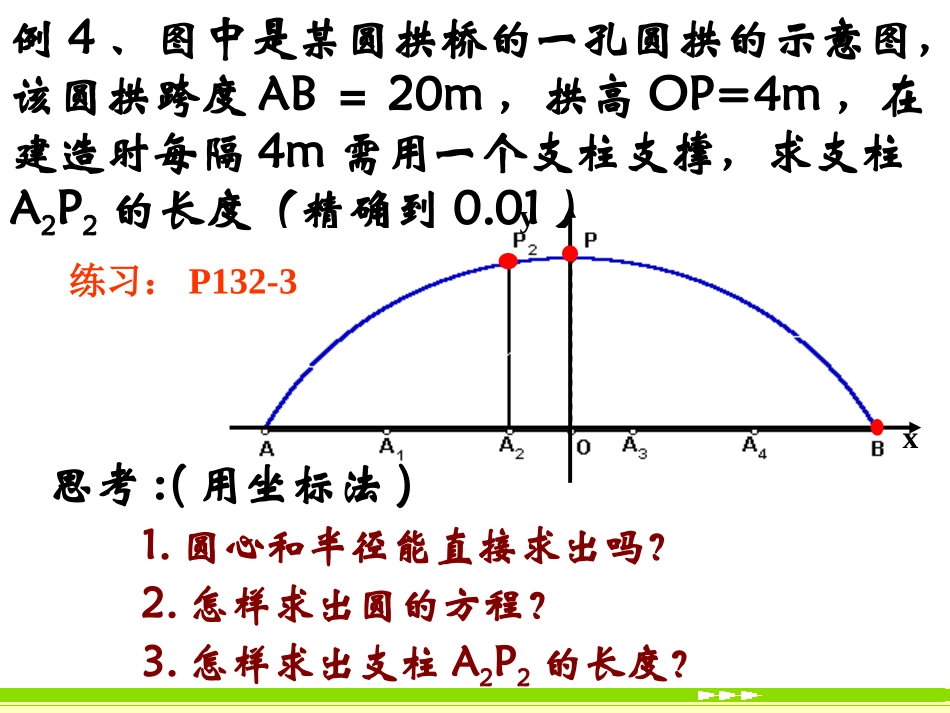
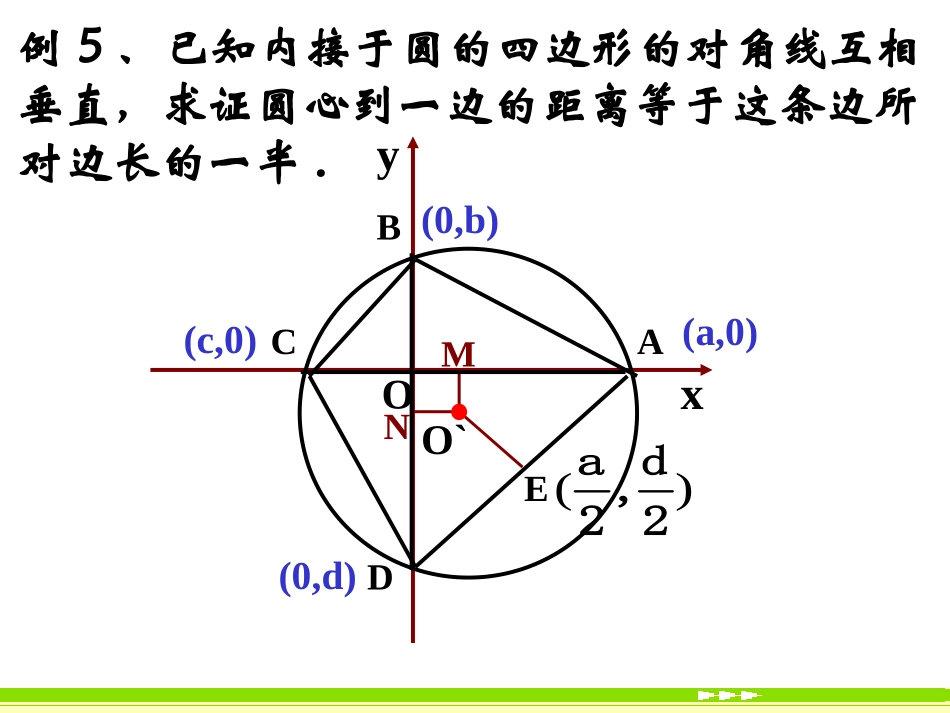
§4.2.3§4.2.3直线与圆的方程的应用直线与圆的方程的应用例4、图中是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01)yx思考:(用坐标法)1.圆心和半径能直接求出吗?2.怎样求出圆的方程?3.怎样求出支柱A2P2的长度?练习:P132-3E例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.xyOCABD(a,0)(0,b)(c,0)(0,d)O`)(2d,2aMN第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论.练习:P132-4oyx(6,0)(2,0)(0,0)ABDCEP)33,3()3,5(1133ABCDEBCACBDBCCECAADBEPAPCP练习:等边中,点,分别在边,上,且,,相交于点,求证6练习3:P133—B组1(1)怎样建系;(2)如何求点C的坐标。练习3:P133—B组2练习4、点M在圆心为C1的方程:x2+y2+6x-2y+1=0,点N在圆心为C2的方程x2+y2+2x+4y+1=0,求|MN|的最大值.