第一章133二项式定理的应用VIP免费

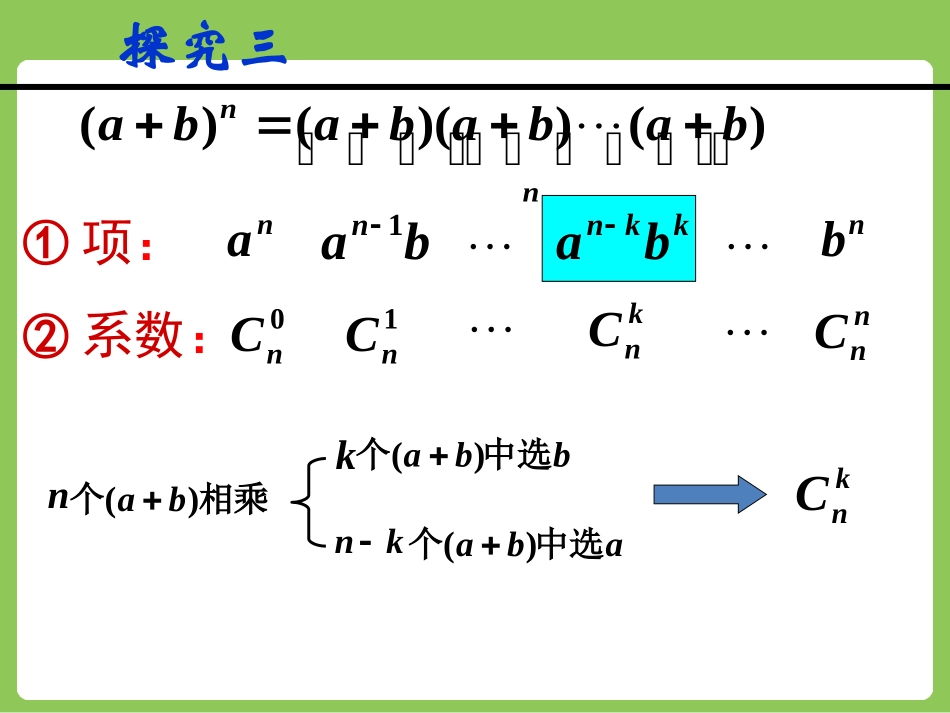
1.3.3二项式定理的应用探究请按照乘法的运算律把下列式子展开?)(3ba?)(2ba222baba()()ababab4()?ab432234464aabababb你能猜想(a+b)n的展开式吗？322333aababb()()()()ababababnnbabababa)())(()(①项：②系数：0nC1nCnnCknCnaban1kknbanb探究三相乘个)(banaba中选个)(knbba中选个)(kknC④二项展开式的通项:1kT③二项式系数:(0,1,2,,)knCkn①项数：②次数：共有n＋1项各项的次数都等于n，kknknbaC)()(*110NnbCbaCbaCaCbannnkknknnnnnn字母a按降幂排列，次数由n递减到0,字母b按升幂排列，次数由0递增到n.⑤a与b之间用加号连接二项式定理二项式定理)()(*110NnbCbaCbaCaCbannnkknknnnnnn?)(nba011[()]()()()nnnknkknnnnnnabCaCabCabCb二项式定理二项式定理例1.126的展开式求xx661212xxxx解63121xx法一：直接展开法二：先化简再运用公式61524336663)(2)(2)(2)xCxCxCxx1=[(24256666(2)(2)]CxCxC32236012164192240160xxxxxx=题型一：二项展开式的的正用和逆用例2例3求712x的展开式的第4项；并写出第4项的二项式系数及第4项的系数；变式1：求712x的展开式的倒数第4项题型二：求二项式展开式的特定项第4项的二项式系数为3735C变式2：求712x的展开式的中间两项；变式3：思考712x展开式的第4项与721x展开式的第4项相同吗？题型二：求二项式展开式的特定项课堂练习66书本第31页书本第37页A组第8题8.已知(1)nx的展开式中第4项与第8项的二项式系数相等，求这两项的二项式系数。例4已知3312nxx的展开式中第６项为常数项．(1)求n;(2)求含2x的项的系数;(3)求展开式中所有的有理项.1）注意二项式定理中二项展开式的特征2）区别二项式系数，项的系数3）掌握用通项公式求二项式系数，项的系数及项小结思考：1.试求(x+2y+z)6的展开式中含xy2z3项的系数.2.若()()5112axxxx展开式中的常数项为－40，则a=(2016年理科省质检第15题)