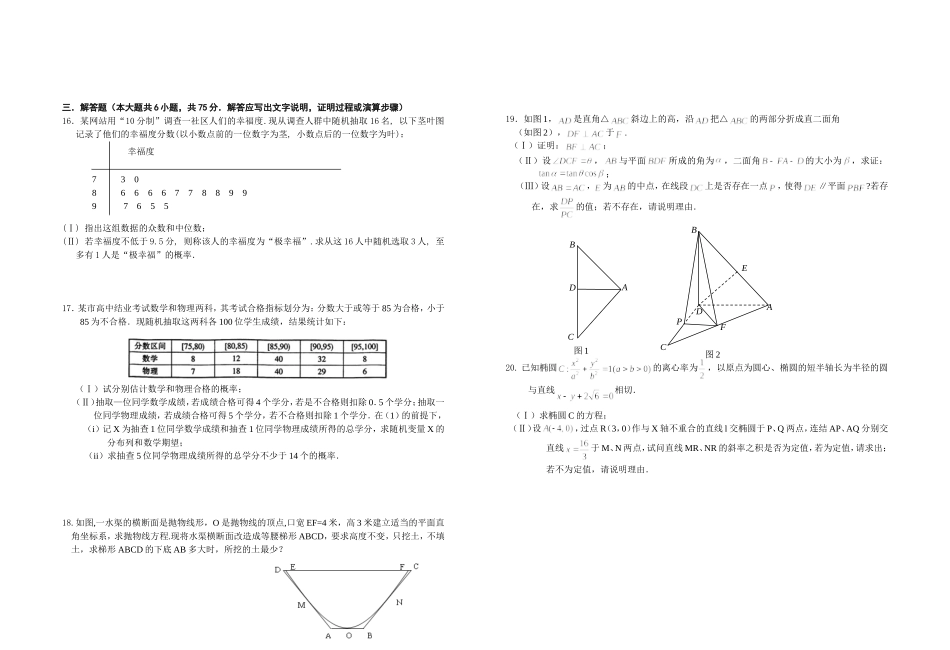
龙泉中学2014年高二理科数学周练(20)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,选出符合题目要求的一项.)1.若复数满足i,其中i为虚数单位,则的虚部为()A.B.C.D.2.“”是“xy>0”成立的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.对两个变量和进行回归分析,得到一组样本数据:则下列说法中不正确的是()A.由样本数据得到回归方程为必过样本点的中心B.残差平方和越小的模型,拟合的效果越好C.若变量和之间的相关系数,则变量和之间具有线性相关关系D.用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好4.的展开式中的常数项为()A.12B.C.D.5.如果执行下面的程序框图,那么输出的S=()A.2450B.2500C.2550D.26526.总体由编号分别为01,02,…,19,20的20个个体组成。利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为()7816657208026314070243699728019832049234493582003623486969387481A.B.C.D.7.曲线与坐标周围成的面积()A.4B.2C.3D.8.直线1l与2l都经过原点o,1l与2l分别交椭圆2222yx于CA,与DB,,且1l2l,则四边形ABCD的面积的取值范围是()A.B.C.D.9.函数(其中是自然对数的底数)的图象上存在点满足条件:,则实数的取值范围是()A.B.C.D.二.填空题(本大题共5小题,每小题5分,共25分.)11.已知正三角形内切圆的半径与它的高的关系是:,把这个结论推广到空间正四面体,则正四面体内切球的半径与正四面体高的关系是________.12.把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”则)(ABP=.13.设,若,则的最大值为.14.6张卡片上分别写有数字1,1,2,3,4,5,从中取4张排成一排,可以组成不同的4位奇数的个数为______.(用数字作答)15.已知双曲线中,是左、右顶点,是右焦点,是虚轴的上端点.若在线段上(不含端点)存在不同的两点,使得△构成以为斜边的直角三角形,则双曲线离心率的取值范围是.yxOA1A2BF三.解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤)16.某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):幸福度7308666677889997655(Ⅰ)指出这组数据的众数和中位数;(Ⅱ)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率.17.某市高中结业考试数学和物理两科,其考试合格指标划分为:分数大于或等于85为合格,小于85为不合格.现随机抽取这两科各100位学生成绩,结果统计如下:(Ⅰ)试分别估计数学和物理合格的概率;(Ⅱ)抽取—位同学数学成绩,若成绩合格可得4个学分,若是不合格则扣除0.5个学分;抽取一位同学物理成绩,若成绩合格可得5个学分,若不合格则扣除1个学分.在(1)的前提下,(i)记X为抽查1位同学数学成绩和抽查1位同学物理成绩所得的总学分,求随机变量X的分布列和数学期望;(ii)求抽查5位同学物理成绩所得的总学分不少于14个的概率.18.如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米建立适当的平面直角坐标系,求抛物线方程.现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少?19.如图1,是直角△斜边上的高,沿把△的两部分折成直二面角(如图2),于.(Ⅰ)证明:;(Ⅱ)设,与平面所成的角为,二面角的大小为,求证:;(Ⅲ)设,为的中点,在线段上是否存在一点,使得∥平面?若存在,求的值;若不存在,请说明理由.20.已知椭圆的离心率为,以原点为圆心、椭圆的短半轴长为半径的圆与直线相切.(Ⅰ)求椭圆C的方程;(Ⅱ)设,过点R(3,0)作与X轴不重合的直线l交椭圆于P、Q两点,连结AP、AQ分别交直线于M、N两点,试问直线MR、NR的斜率之积是否为定值,若为定值,请求出;...