简单的线性规划--龙泉中学VIP免费

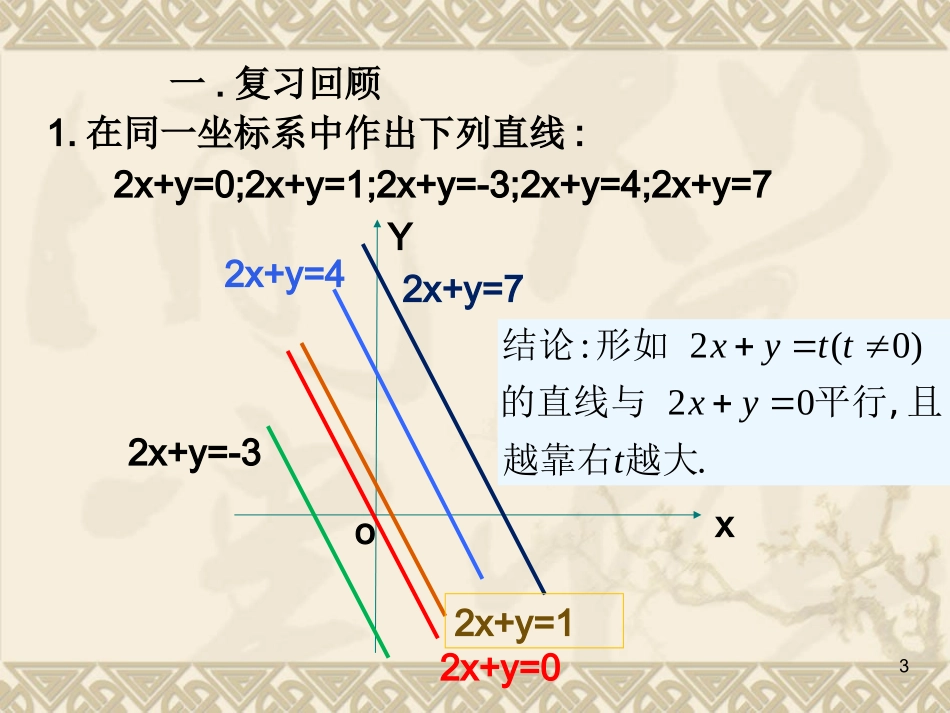
荆门龙泉中学叶子成高中数学23xY一.复习回顾1.在同一坐标系中作出下列直线:2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7:2(0)20.xyttxyt结论形如的直线与平行,且越靠右越大o2x+y=02x+y=12x+y=-32x+y=42x+y=7(0)00.AxByttAxByAt一般地，形如的直线与平行,当时，越靠右,越大4xYoAx+By=0Ax+By=t1Ax+By=t2120tt52.作出下列不等式组的所表示的平面区域1255334xyxyx655x=1x-4y+3=03x+5y-25=01ABCC:(1,4.4)A:(5,2)B:(1,1)Oxy问题1：x有无最大（小）值？问题2：y有无最大（小）值？问题3：2x+y有无最大（小）值？1255334xyxyx2.作出下列不等式组的所表示的平面区域7二.提出问题把上面两个问题综合起来:1255334xyxyx设z=2x+y,当x,y满足时,求z的最大值和最小值.855x=1x-4y+3=03x+5y-25=01ABCC:(1.00,4.40)A:(5.00,2.00)B:(1.00,1.00)Oxy.1255334.1所表示的区域先作出xyxyx02yx02:.20yxl作直线03.:2,zllxyzR作一组与直线平行的直线直线l越往右平移,z随之增大.以经过点A(5,2)的直线所对应的z值最大;经过点B(1,1)的直线所对应的z值最小.3112,12252minmaxZZ可以通过比较(x,y)所在区域边界顶点处的函数z值大小得到。思考：还可以运用怎样的方法得到目标函数的最大、最小值？9线性规划问题：设z=2x+y，式中变量满足下列条件：求z的最大值与最小值。1255334xyxyx目标函数（线性目标函数）线性约束条件CBAx=1x-4y+3=03x+5y-25=0xOy象这样关于x,y一次不等式组的约束条件称为线性约束条件Z=2x+y称为目标函数,(因这里目标函数为关于x,y的一次式,又称为线性目标函数10线性规划线性规划：求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题．可行解：满足线性约束条件的解(x，y)叫可行解；可行域：由所有可行解组成的集合叫做可行域；最优解：使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。可行域2x+y=32x+y=12(1,1)(5,2)(x,y)111255334xyxyx设z=2x+y,当x,y满足时,求z的最大值和最小值.线性目标函数线性约束条件线性规划问题任何一个满足不等式组的（x,y）可行解可行域所有的最优解这里目标函数所表示的几何意义——在y轴上的截距。12典型例题例1解下列线性规划问题：求z=2x+y的最大值和最小值，使式中x、y满足下列条件：11yyxxy解线性规划问题的一般步骤：第一步：在平面直角坐标系中作出可行域；第二步：在可行域内找到最优解所对应的点；第三步：解方程得最优解，从而求出目标函数的最大值或最小值。C(12,12)B(2,-1)A(-1,-1)xOy2x+y=02x+y=-32x+y=3答案：当x=-1,y=-1时，z=2x+y有最小值－3.当x=2,y=-1时，z=2x+y有最大值3.也可以通过比较可行域边界顶点的目标函数值大小得到。线性规划例2解下列线性规划问题：求z=300x+900y的最大值和最小值，使式中x、y满足下列条件：x+3y=0300x+900y=0300x+900y=112500答案：当x=0,y=0时，z=300x+900y有最小值0.当x=0,y=125时，z=300x+900y有最大值112500.0025023002yxyxyxC125250150BAx+2y=2502x+y=300xOy14练习(1)已知求z=2x+y的最大值和最小值。01y01-yx0y-x15551Oxyx-y=0x+y-1=01-1y+1=0A(2,-1)B(-1,-1)max2213.zmin3z类似可得解:作出可行域(如图阴影部分)0:20lxy作直线01llAz将直线向右平移到时，经过可行域中的点（2，-1），且离原点最远.此时最大0l1l2l16例3:某工厂用A,B两种配件生产甲,乙两种产品,每生产一件甲种产品使用4个A配件耗时1h,每生产一件乙种产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8小时计算,该厂所有可能的日生产安排是什么?若生产1件甲种产品获利2万元,生产1件乙种产品获利3万元,采用哪种生产安排利润最大?把例1的有关数据列表表示如下:32利润(万元)821所需时间1240B种配件1604A种配件资源限额乙产品(1件)甲产品(1件)产品资源消耗量资源172841641200xyxyxy...