三垂线定理及逆定理（一）newVIP免费

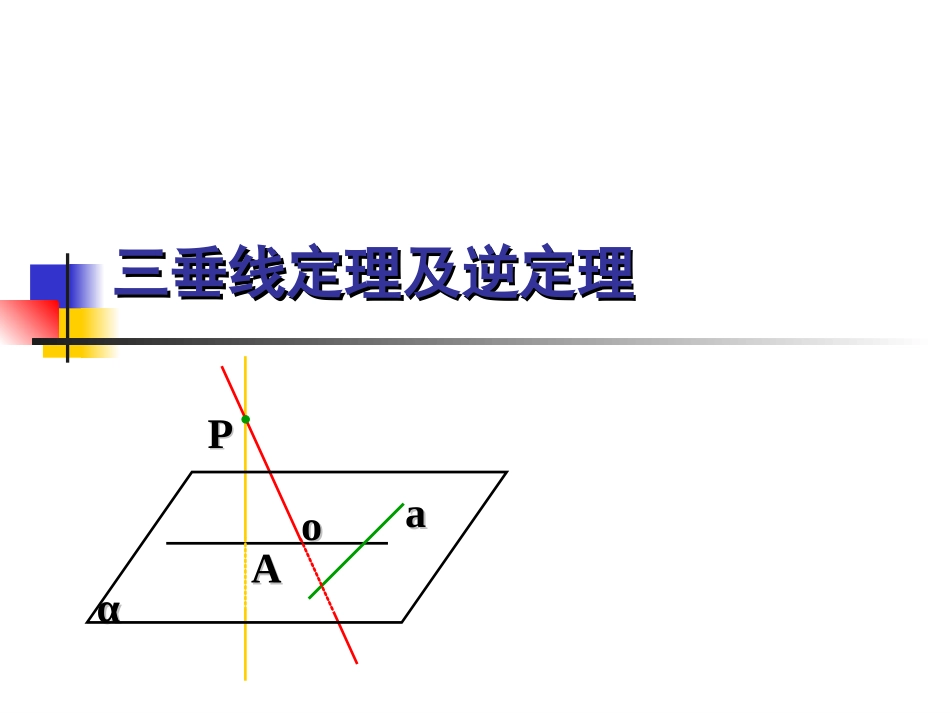
三垂线定理及逆定理三垂线定理及逆定理aaAAPPooαα[思考]如图，是平面α的一条斜线，如何在α内画一条直线与垂直？llαlaAAPOαla.--------aOAaaPAPO.--------aPAaaOAPO:aPA,aOA,PO三垂线逆定理三垂线定理其中涉及到三对垂直关系：OA是PA在平面α内的射影OA是PA在平面α内的射影三垂线定理：三垂线定理：在平面内的一条直线，如果它和在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直这条斜线垂直..aaAAPPooαα已知已知:PA:PA、、POPO分别是平面分别是平面αα的垂的垂线、斜线，线、斜线，AOAO是是POPO在平面在平面αα内的内的射影，且射影，且aαaα，，a⊥AOa⊥AO求证：求证：a⊥POa⊥PO三垂线逆定理：三垂线逆定理：在平面内的一条直线，如果它在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直斜线在平面内的射影垂直..aaAAPPooααaaAAPPooαα理解和深化理解和深化⒈为什么称为“三垂线”定理？三种垂直关系:①线面垂直②线射垂直③线斜垂直⒉这个定理的作用是什么？三垂线定理三垂线定理实质是平面内的直线和平面的斜线垂直的判定定理.3.如果将定理中“在平面内”的条件去掉，结论成立吗？AAPPooααa直线a必须要在平面内,如果a不在平面内,定理就不一定成立.ADCBA1D1B1C1练习:(1)求证:(2)求证:CBBD11CABBD11平面解题反思ABCDO[[思考思考1]:1]:在四面体在四面体A-BCDA-BCD中中,A,A在平在平面面BCDBCD中的射影中的射影OO在△在△BCBCDD内内,,试根据下列条件试根据下列条件,,判断判断OO为△为△BCDBCD的什么心的什么心??(1)A(1)A到△到△BCDBCD的三边距离相等的三边距离相等..(2)AB=AC=AD.(2)AB=AC=AD.(3)AB,AC,AD(3)AB,AC,AD两两垂直两两垂直..ABCDO在四面体在四面体A-BCDA-BCD中中.,,BDACADBCCDAB求证：若[[思考思考2]:2]:ADCBA1D1B1C1MOP若O为中心,P为上一点,M为CD中点.求证：PO⊥AM11BCCBDD1N[[思考思考3]:3]:ADCBA1D1B1C1EFG解题反思：找出平面的垂线可使思路更加清晰.“作——证——算”三步.若E为的中点,求E到距离.CC1设正方体的棱长为2,1111DCBAABCD1AB[[思考思考4]:4]:思考：若平面思考：若平面αα内的直角△内的直角△ABCABC的斜边的斜边AAB=20,B=20,平面平面αα外一点外一点OO到到AA、、BB、、CC三点三点距离都是距离都是25,25,求：点求：点OO到平面的距离．到平面的距离．小结小结::到目前为止，证明空间两条直线垂直的方法有哪些？①利用定义，证明两条直线所成角是直角.②利用线面垂直的定义.③利用三垂线定理和逆定理.三垂线定理和逆定理是判断线线垂直的重要方法之一，选择平面内直线、平面的斜线及与之对应的射影是问题的核心.先找出平面的垂线可使思路更加清晰.