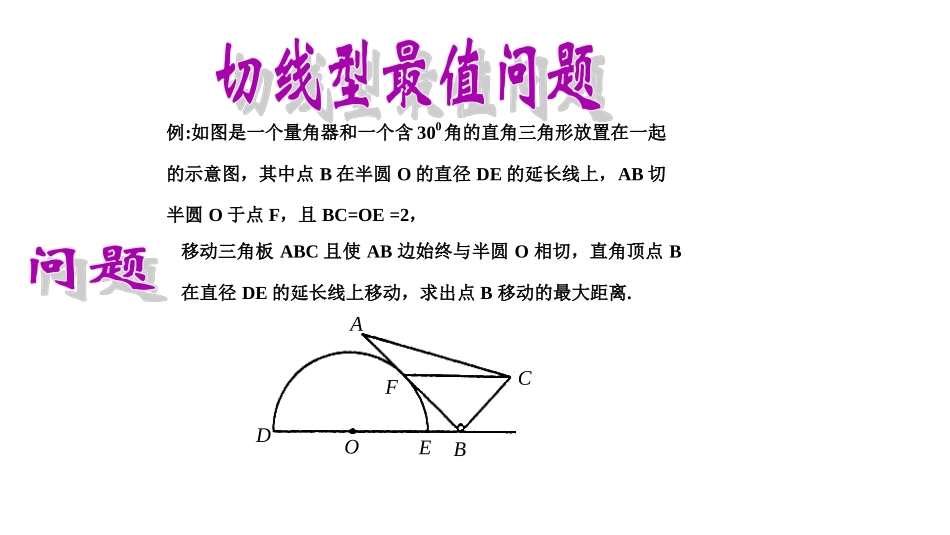
天街小雨润如酥草色遥看近却无最是一年春好处绝胜烟柳满皇都切线型最值问题ABCODFE例:如图是一个量角器和一个含300角的直角三角形放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OE=2,移动三角板ABC且使AB边始终与半圆O相切,直角顶点B在直径DE的延长线上移动,求出点B移动的最大距离.滑动直角三角板使得AB与BD的夹角为45°,即∠ABD=45°;点P是切线AB上的一个动点,当∠DPE的度数最大时,求此刻P到BD的距离.滑动直角三角板使得B与E重合,此刻边BC落在直线DE上;若P是量角器半圆O上的一个动点,连结PC交AB于点Q,求面积的最小值?AQC△滑动直角三角板使得B与E重合,此刻边BC落在直线DE上;若P是量角器半圆O上的一个动点,过P作半圆O的切线交AC于点Q,P为切点,求切线长PQ的最小值?练习1.如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是_________.练习2.在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2,设tanBOC=m∠,则m的取值范围是________.练习3.直线CD与以线段AB为直径的圆相切与点D并交BA的延长线于点C,且AB=AC=2,P点在切线CD上移动.当∠APB的度数最大时,求此刻点P坐标?练习3.直线CD与以线段AB为直径的圆相交于点D、点P并交BA的延长线于点C,且AB=AC=2,Q点在CD上移动.当∠AQB的度数最大时,求此刻点Q坐标?以上例题、变式和练习本质上都是与切线有关的最值问题,解决问题的关键是构造和利用切线,结合数形结合思想、转化思想,更多地体现在对解题策略的思考上。我们通过作图从直观上得到猜想,再通过说理、计算将问题上升到理性认识。