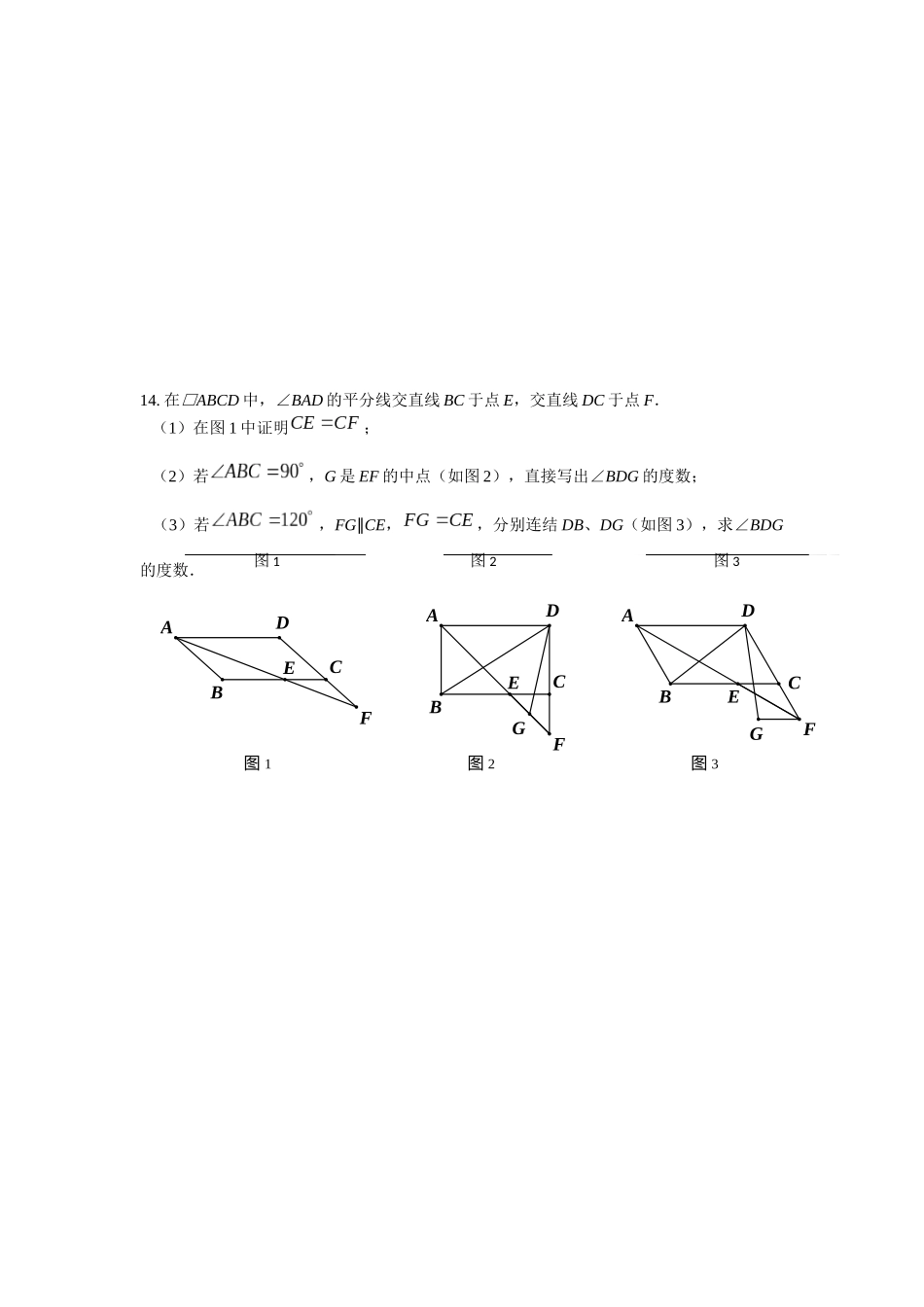
第6题图第9题图第11题图2016年郴州市能力竞赛试卷样卷初中数学(试题卷)本试卷共*页,有3道大题,16小题,满分130分,考试时间120分钟.一、选择题(本大题共6小题,每小题5分,共30分)1.5张不同卡片分别写有数字2,3,4,5,6,从中任意取出3张,则这三张卡片上所写的数字可以作为三角形的三边长的概率是A.B.C.D.2.点P是直线x+y−4=0上一动点,O为原点,则|OP|的最小值为A.2B.√2C.2√2D.43.已知abc≠0,并且a+bc=b+ca=c+ab=p,则直线y=px+p一定经过A.第一、三象限B.第二、三象限C.第三、四象限D.第一、四象限4.已知,则A.B.C.D.5.如果,那么|x−a|+|x+2014|+|x−a+2014|的最小值是A.2014B.a+2014C.4028D.a+40286.如图,为等腰三角形内一点,过分别作三条边、、的垂线,垂足分别为、、.已知,,且.则四边形的面积为A.10B.15C.D.二、填空题(本大题共6小题,每小题5分,共30分)7.已知则___________.8.分解因式:(x2+3x−3)(x2+3x+4)−8=.9.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图方式放置,点A1,A2,A3…和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上.已知点B1(1,1),B2(3,2),请写出点Bn的坐标是.10.已知直线与抛物线交于,两点,则.11.如图,已知正方形的边长为1,点,分别在边,上,且,则的周长为.12.若时,二次函数的最小值为,则.三、解答题(13~14每题15分,15~16每题20分,共70分)13.若关于的二次函数与轴的两个交点的横坐标分别是,试求的最小值.GFEDACB图2GFEDACBFEDACB图1图3GFEDACBGFEDACBFEDACB图1图2图314.在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明;(2)若,G是EF的中点(如图2),直接写出∠BDG的度数;(3)若,FG∥CE,,分别连结DB、DG(如图3),求∠BDG的度数.15.已知一次函数的图象与轴,轴分别相交于A,B两点,点P在该函数图象上,P到轴,轴的距离分别为,.(1)当P为线段AB的中点时,求的值;(2)直接写出的范围,并求当时点P的坐标;(3)若在线段AB上存在无数个P点,使(为常数),求的值.16.如图,在平面直角坐标系中,A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E.已知CD=8,抛物线经过O,E,A三点.(1)求直线OB的函数表达式;(2)求抛物线的函数表达式;(3)若P为抛物线上位于第一象限内的一个动点,以P,O,A,E为顶点的四边形面积记作S,则S取何值时,相应的点P有且只有3个.2016年郴州市能力竞赛试卷样卷初中数学参考答案一、选择题(本大题共6小题,每小题5分,共30分)1.B2.C3.B若a+b+c≠0,由等比性质可知:若a+b+c=0,则a+b=-c,4.A解析:由,知,,,.∴.第6题答图5.A6.C解析:如图,连结,,.易知,∴,,由知点在的平分线上,、、三点共线.∴∴∴二、填空题(本大题共6小题,每小题5分,共30分)7.288.(x−1)(x+4)(x2+3x+5)9.()10.解析:由,得①,依题意,,为方程①的两根,∴∴.第11题答图11.2解析:如图,在的延长线上取点,使得,连结则由为正方形,易得∴, ,∴于是,在与中,,,∴,的周长12.5解析: ,,∴若,即时,则当时,取最小值.由知,,不符合要求.若,即时,则当时,取最小值由知,,得,均不符合要求.若,即时,则当时,取最小值.由知,,符合要求.∴.三、解答题(13~14每题15分,15~16每题20分,共70分)13.解:由题意知:为方程的两根,= △,∴.由韦达定理得:∴当时,函数值随m值得增大而减小,∴当时,.当时,函数值随m值得增大而增大,∴当时,.综上,的最小值为8.14.(1)证明:如图1. AF平分BAD,∴BAF=DAF, 四边形ABCD是平行四边形,∴AD//BC,AB//CD。∴DAF=CEF,BAF=F,∴CEF=F,∴CE=CF.(2)BDG=45°.(3)分别连结GB、GE、GC(如图2). AB//DC,ABC=120°,∴ECF=ABC=120°, FG//CE且FG=CE,∴四边形CEGF是平行四边形.由(1)得CE=CF,∴□CEGF是菱形,∴EG=EC,GCF=GCE=12ECF=60°.∴△ECG是等边三角形.∴EG=CG,GEC=EGC=60°,∴GEC=GCF,FEDACB图1∴BEG=DCG,由AD//BC及AF平...