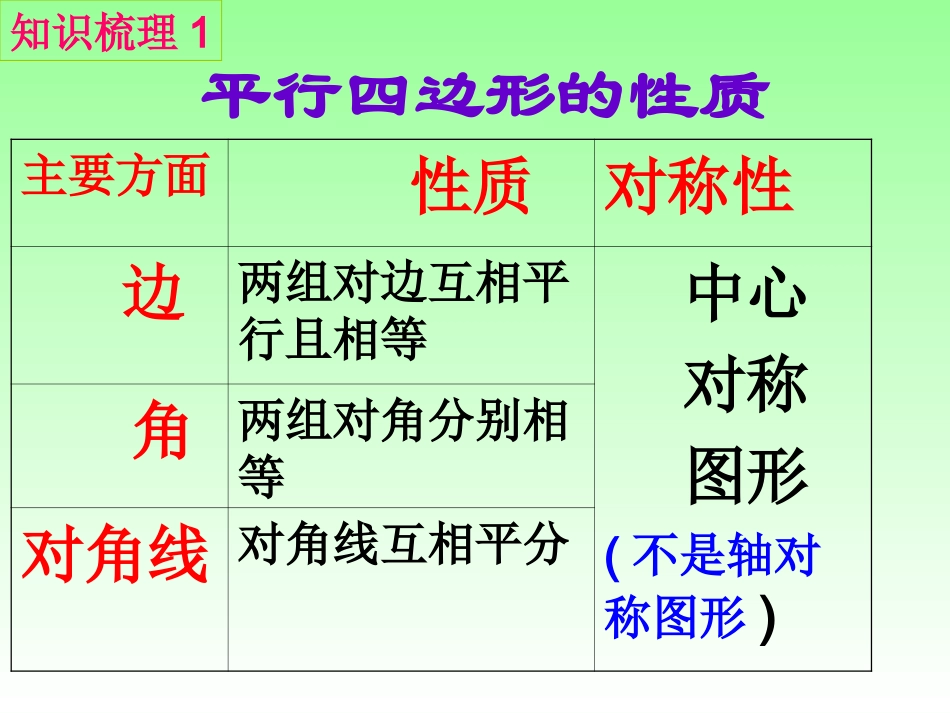
平行四边形的复习课---性质与判定•能熟记平行四边形的性质和判定定理;•会运用平行四边形的性质和判定定理解决一些几何计算和推理题,培养学生的综合运用能力。学习目标主要方面性质对称性边两组对边互相平行且相等中心对称图形(不是轴对称图形)角两组对角分别相等对角线对角线互相平分平行四边形的性质知识梳理1平行四边形的判定方法边1.两组对边分别平行的四边形是……2.两组对边分别相等的四边形是……3.一组对边平行且相等的四边形是……对角线4.对角线互相平分的四边形是……知识梳理21.1.如图,如图,ABCDABCD的对角线的对角线ACAC,,BDBD相交相交于点于点OO。已知。已知AB=5cmAB=5cm,△,△AOBAOB的周长的周长和△和△BOCBOC的周长相差的周长相差3cm3cm,则,则ADAD的长为的长为____________________ABCDOO2cm2cm小试牛刀2.如图,在ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是_________.ODBAC●1<AD<93、ABCD中,∠A=150°,AB=8cm,BC=10cm,求:四边形ABCD的面积ABCDE解:过点A作AEBC⊥交BC于E。∵四边形ABCD是平行四边形,∴ADBC∥∴∠BAD+B=180∠°∵∠BAD=150°∴∠B=30°在RtABE⊿中,∠B=30°∴AE=AB=4,∴SABCD=4×10=40(cm)214.如图在ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BMBDCEFAM证明:∵四边形BEFM是平行四边形∴BM=EFAB//EF∵AD平分∠BA∴∠BAD=∠CAD∵AB//EF∴∠BAD=∠AEF∴∠CAD=∠AEF∴AF=EF∴AF=BM1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形DABCEF初露锋芒1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且BEDF∥求证:四边形BFDE是平行四边形DOABCEF初露锋芒变式2已知:E、F是平行四边形ABCD对角线AC上的两点,并且求证:四边形BFDE是平行四边形DABCEFBEAC⊥于E,DFAC⊥于F驶向胜利的彼岸11、已知:如图,在平行四边形ABCD中,E,、已知:如图,在平行四边形ABCD中,E,F分别是AB,DC上的两点,且AE=CF.F分别是AB,DC上的两点,且AE=CF.求证:BD,EF互相平分.求证:BD,EF互相平分.要证:BD,EF互要证:BD,EF互相平分,只须证明四相平分,只须证明四边形边形DEBFDEBF为平行四为平行四边形。边形。由已知条件可选择由已知条件可选择DF∥EBDF∥EB且且DF=EBDF=EB大显身手OOFADCBEo变式2、如图:在平行四边形ABCD中,E、F、G、H分别是各边上的点,且AE=CF,BG=DH。求证:EF与GH互相平分。DCABHFGE33、已知:如图,在平行四边形ABCD中,、已知:如图,在平行四边形ABCD中,O是AC的中点,经过点O的直线交AB,O是AC的中点,经过点O的直线交AB,CD于点E,F,交AD,CB的延长线于CD于点E,F,交AD,CB的延长线于点M,N.点M,N.求证:求证:AN∥CMAN∥CM要证明要证明只须证明四边形只须证明四边形ANCMANCM是平行四是平行四边形边形由条件可得由条件可得OA=OCOA=OC因此只须证因此只须证OM=ON,OM=ON,这可由△这可由△AOMAOM≌≌CON△CON△得到得到NADBCMFEO如图:分别以平行四边形ABCD的边BC、CD为边作等边三角形△BCP和△CDQ,求证:△APQ是等边三角形。ADBCPQ能力挑战通过这节课的复习,通过这节课的复习,你又增加了哪些收获?你又增加了哪些收获?能与大家一起分享吗?能与大家一起分享吗?丰收园如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于点F,那么BE=CF,请你说明理由.ABCDEF过关斩将作业:•P82习题8.31,2•P97A:1,3