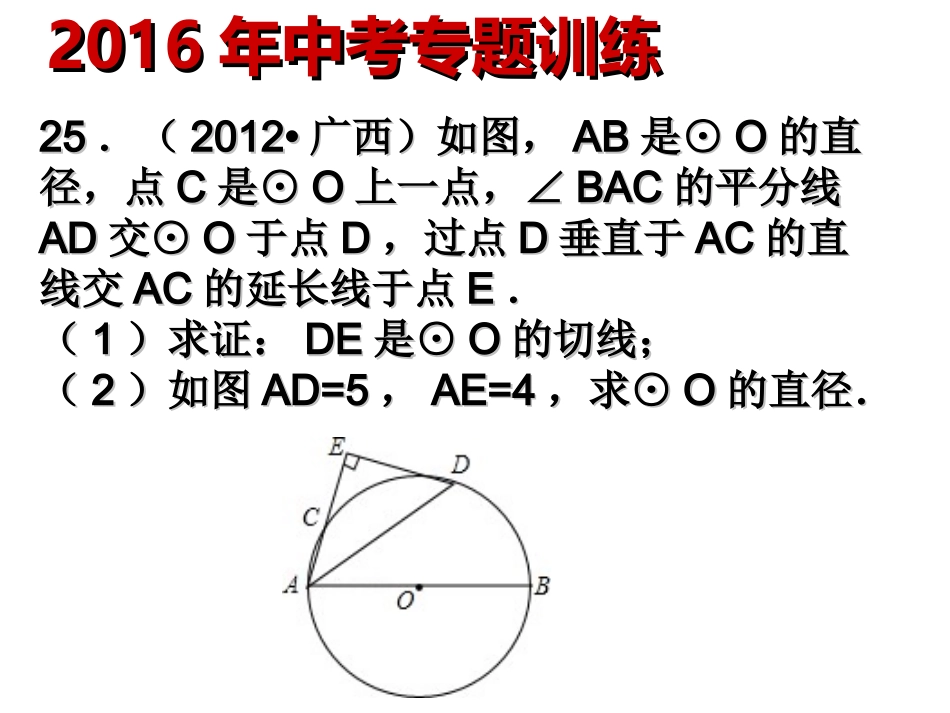
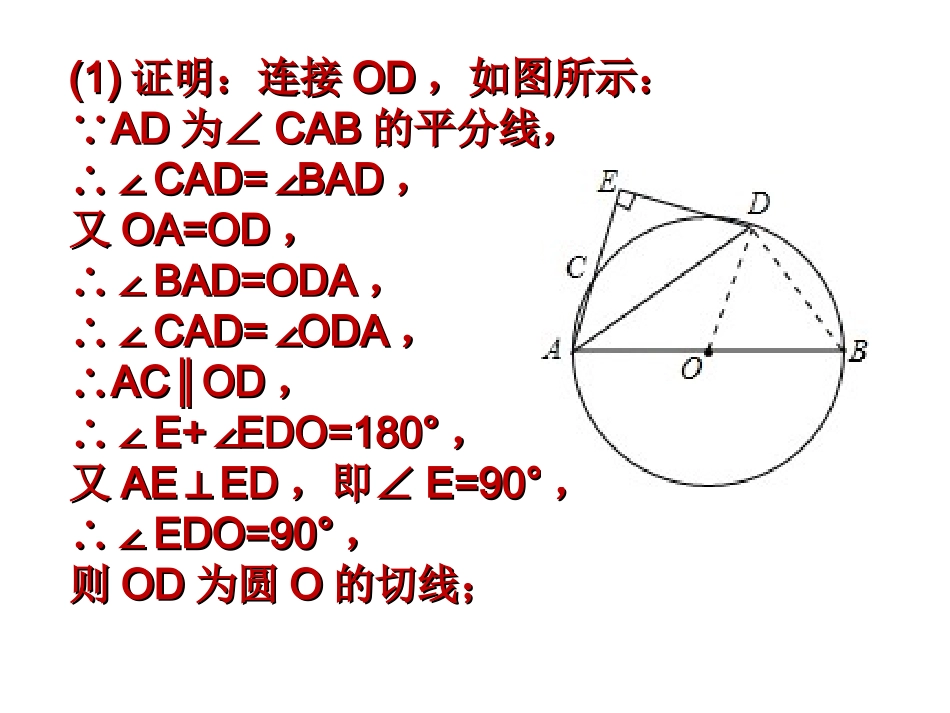
2525.(.(2012•2012•广西)如图,广西)如图,ABAB是是⊙⊙OO的直的直径,点径,点CC是是⊙⊙OO上一点,上一点,∠∠BACBAC的平分线的平分线ADAD交交⊙⊙OO于点于点DD,过点,过点DD垂直于垂直于ACAC的直的直线交线交ACAC的延长线于点的延长线于点EE..((11)求证:)求证:DEDE是是⊙⊙OO的切线;的切线;((22)如图)如图AD=5AD=5,,AE=4AE=4,求,求⊙⊙OO的直径.的直径.20162016年中考专题训练年中考专题训练(1)(1)证明:连接证明:连接ODOD,如图所示:,如图所示:∵∵ADAD为为∠∠CABCAB的平分线,的平分线,∴∠∴∠CAD=BAD∠CAD=BAD∠,,又又OA=ODOA=OD,,∴∠∴∠BAD=ODABAD=ODA,,∴∠∴∠CAD=ODA∠CAD=ODA∠,,∴∴ACOD∥ACOD∥,,∴∠∴∠E+EDO=180°∠E+EDO=180°∠,,又又AEED⊥AEED⊥,即,即∠∠E=90°E=90°,,∴∠∴∠EDO=90°EDO=90°,,则则ODOD为圆为圆OO的切线;的切线;(2)(2)解:连接解:连接BDBD,如图所示,,如图所示,∵∵ABAB为圆为圆OO的直径,的直径,∴∠∴∠ADB=90°ADB=90°,,在在RtABD△RtABD△中,中,cosDAB=∠cosDAB=∠,,在在RtAED△RtAED△中,中,AE=4AE=4,,AD=5AD=5,,∴∴cosEAD==∠cosEAD==∠,又,又∠∠EAD=DAB∠EAD=DAB∠,,∴∴cosDAB=cosEAD==∠∠cosDAB=cosEAD==∠∠,,则则AB=AD=AB=AD=,,即即圆的直径为圆的直径为..2626.(.(2012•2012•广西)已知抛物线广西)已知抛物线y=axy=ax22+2x+c+2x+c的图象与的图象与xx轴交于点轴交于点AA((33,,00)和点)和点CC,,与与yy轴交于点轴交于点BB((00,,33).).((11)求抛物线的解析式;)求抛物线的解析式;((22)在抛物线的对称轴上)在抛物线的对称轴上找一点找一点DD,使得点,使得点DD到点到点BB、、CC的距离之和最小,并的距离之和最小,并求出点求出点DD的坐标;的坐标;((33)在第一象限的抛物线)在第一象限的抛物线上,是否存在一点上,是否存在一点PP,使得,使得△△ABPABP的面积最大?若存在,求出点的面积最大?若存在,求出点PP的坐标;的坐标;若不存在,请说明理由.若不存在,请说明理由.解:(解:(11))∵∵抛物线抛物线y=axy=ax22+2x+c+2x+c的图象经过点的图象经过点AA((33,,00)和点)和点BB((00,,33),),∴∴解得解得a=a=﹣﹣11,,c=3c=3,,∴∴抛物线的解析式为:抛物线的解析式为:y=y=﹣﹣xx22+2x+3+2x+3..((22)对称轴为)对称轴为x==1x==1,,令令y=y=﹣﹣xx22+2x+3=0+2x+3=0,,解得解得xx11=3=3,,xx22==﹣﹣11,,∴∴CC(﹣(﹣11,,00).).如图如图11所示,连接所示,连接ABAB,与对称轴,与对称轴x=1x=1的交点即为所求之的交点即为所求之DD点,由于点,由于AA、、CC两点关于两点关于对称轴对称,则此时对称轴对称,则此时DB+DC=DB+DA=ABDB+DC=DB+DA=AB最小.最小.设直线设直线ABAB的解析式为的解析式为y=kx+by=kx+b,,由由AA((33,,00)、)、BB((00,,33)可得)可得解得解得k=k=﹣﹣11,,b=3b=3,,∴∴直线直线ABAB解析式为解析式为y=y=﹣﹣x+3x+3..当当x=1x=1时,时,y=2y=2,,∴∴DD点坐标为(点坐标为(11,,22).).((33)结论:存在.)结论:存在.如图如图22所示所示,,设设PP((xx,,yy)是第一象限的抛物线上一点)是第一象限的抛物线上一点,,过点过点PP作作PN⊥xPN⊥x轴于点轴于点NN,,则则ON=xON=x,,PN=yPN=y,,AN=OAAN=OA﹣﹣ON=3ON=3﹣﹣x.x.SS△△ABPABP=S=S梯形梯形PNOBPNOB+S+S△△PNAPNA﹣﹣SS△△AOBAOB==((OB+PNOB+PN))••ON+PN•ANON+PN•AN﹣﹣OA•OBOA•OB==((3+y3+y))••x+y•x+y•((33﹣﹣xx))﹣﹣×3×3×3×3==((x+yx+y))﹣﹣∵∵PP((xx,,yy)在抛物线上)在抛物线上,,∴∴y=y=﹣﹣xx22+2x+3+2x+3,,代入上式得代入上式得SS△△ABPABP==((x+yx+y))﹣﹣==﹣﹣((xx22﹣﹣3x3x))==﹣﹣((xx﹣﹣))22++∴∴当当x=x=时时,,SS△△ABPABP取得最大值.取得最大值.当当x=x=时时,,y=y=﹣﹣xx22+2x+3=+2x+3=,,∴∴PP((,,).).所以所以,,在第一象限的抛物线上在第一象限的抛物线上,,存在一点存在一点PP,,使得使得△△ABPABP的的面积最大面积最大;;PP点的坐标为(点的坐标为(,,).).