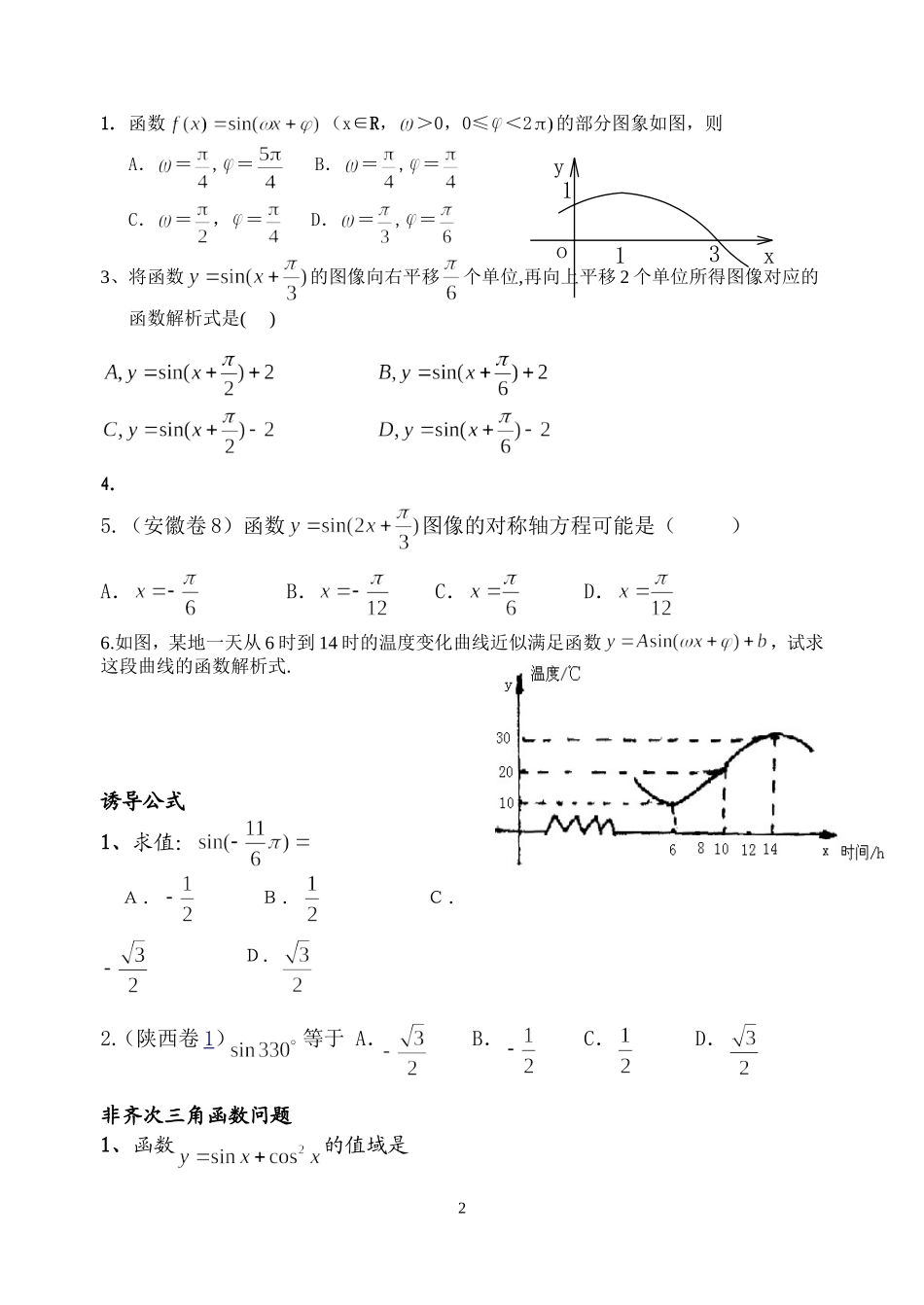
必修四知识点分类复习三角函数定义与同角函数基本关系1.若是第二象限的角,且,则()A.B.C.D.2、已知,且是第四象限的角,则()A.B.C.D.设集合3.(重庆卷)已知,,则。4.(北京卷)已知=2,求(I)的值;(II)的值.5.(湖南)三角函数的图像与解析式11.函数(x∈R,>0,0≤<2的部分图象如图,则A.=,=B.=,=C.=,=D.=,=3、将函数的图像向右平移个单位,再向上平移2个单位所得图像对应的函数解析式是()4.5.(安徽卷8)函数图像的对称轴方程可能是()A.B.C.D.6.如图,某地一天从6时到14时的温度变化曲线近似满足函数,试求这段曲线的函数解析式.诱导公式1、求值:A.B.C.D.2.(陕西卷1)等于A.B.C.D.非齐次三角函数问题1、函数的值域是2131oyxA.B.C.D.齐次三角函数问题1.(江西卷)函数的最小正周期为_______2.(辽宁卷)函数的最小正周期是______3.(全国II)函数y=sin2xcos2x的最小正周期是(A)2π(B)4π(C)(D)5.(上海卷6)函数f(x)=sinx+sin(+x)的最大值是6.广东)已知函数,则的最小正周期是.7.(全国二10).函数的最大值为()A.1B.C.D.28.(广东卷)已知函数.(I)求的最小正周期(II)求的的最大值和最小值;(III)若,求的值.9.(辽宁卷)已知函数,.求:(I)函数的最大值及取得最大值的自变量的集合(II)函数的单调增区间.和差公式1、(13分)已知,求的值.32.(福建卷)已知∈(,),sin=,则tan()等于A.B.7C.-D.-73.(陕西卷)cos43°cos77°+sin43°cos167°的值为4.(重庆卷)已知,sin()=-sin则cos=________.向量的运算与向量的性质1.(安徽卷2)若,,则()A.(1,1)B.(-1,-1)C.(3,7)D.(-3,-7)2.(广东卷)如图1所示,是的边上的中点,则向量A.B.C.D.3.(四川卷3)设平面向量,则()(A)(B)(C)(D)1.(湖南卷)已知向量若时,∥;时,,则A.B.C.D.2.(全国II)已知向量=(4,2),向量=(,3),且//,则=(A)9(B)6(C)5(D)33.(广东卷3)已知平面向量,,且//,则=()A、B、C、D、4.(海南卷5)已知平面向量=(1,-3),=(4,-2),与垂直,则是(4ADCB图1)A.-1B.1C.-2D.2向量的长度和夹角1.(福建卷)已知向量与的夹角为,则等于(A)5(B)4(C)3(D)12.(天津卷)设向量与的夹角为,,,则.3.(江西卷)已知向量,,则的最大值为.4.(上海春)若向量的夹角为,,则.6.(全国II)已知向量a=(sinθ,1),b=(1,cosθ),-<θ<.(Ⅰ)若a⊥b,求θ;(Ⅱ)求|a+b|的最大值.16.(本小题满分12分)已知A、B、C是△ABC的三个内角,向量(1,3),(cos,sin),mnAA�且1.mn�(1)求角A;(2)若221sin23,tansincosBCBB求的值。三角函数板块(答案)三角函数定义与同角函数基本关系1.若是第二象限的角,且,则(D)A.B.C.D.2、已知,且是第四象限的角,则(B)5A.B.C.D.设集合3.(重庆卷)已知,,则。解:由,cos=-,所以-24.(北京卷)已知=2,求(I)的值;(II)的值.解:(I) tan=2,∴;所以=;(II)由(I),tanα=-,所以==.5.(2004年湖南高考数学·文史第17题,本小题满分12分)6解:由于是三角函数的图像与解析式1.函数(x∈R,>0,0≤<2的部分图象如图,则B7A.=,=B.=,=C.=,=D.=,=2、已知函数的图像关于直线对称,则的值是.2.答案-1解:依设有f(-α)=f(+α),令α=,得f(0)=f(),∴-k=1,∴k=-13、将函数的图像向右平移个单位,再向上平移2个单位所得图像对应的函数解析式是()B4.(北京卷)函数y=1+cosx的图象(A)关于x轴对称(B)关于y轴对称(C)关于原点对称(D)关于直线x=对称解:函数y=1+cos是偶函数,故选B5.(安徽卷8)函数图像的对称轴方程可能是(D)A.B.C.D.诱导公式1、求值:()A.B.C.D.8131oyx1.答案B解:原式=sin(-2π+)=sin=.2.(陕西卷1)等于(B)A.B.C.D.非齐次三角函数问题1、函数的值域是A.B.C.D.解:y=sinx+1-sin2x=-(sinx-)2+, sinx∈[-1,1],∴sinx=时,ymax=,又sinx=-1时,ymin=-1∴值域为[-1,]齐次三角函数问题1.(江西卷)函数的最小正周期为...