三角基础知识VIP免费

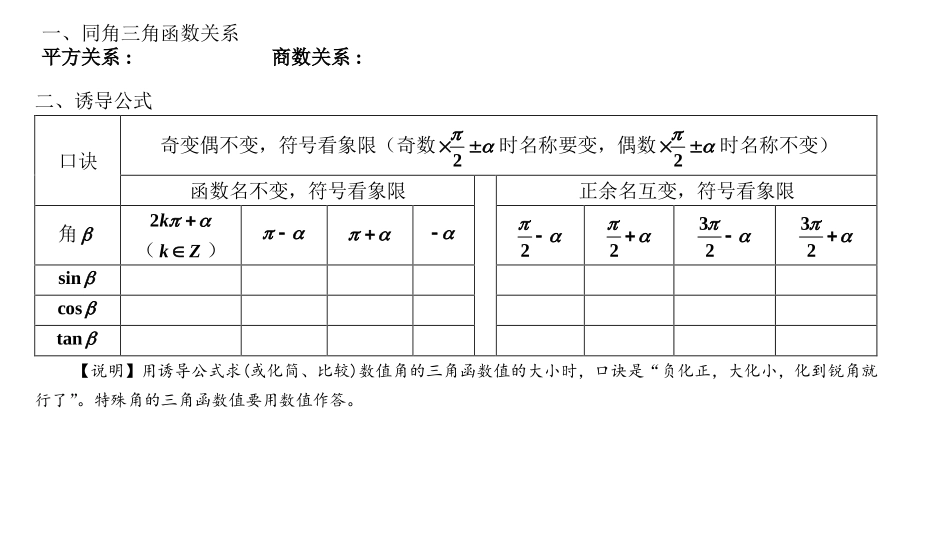
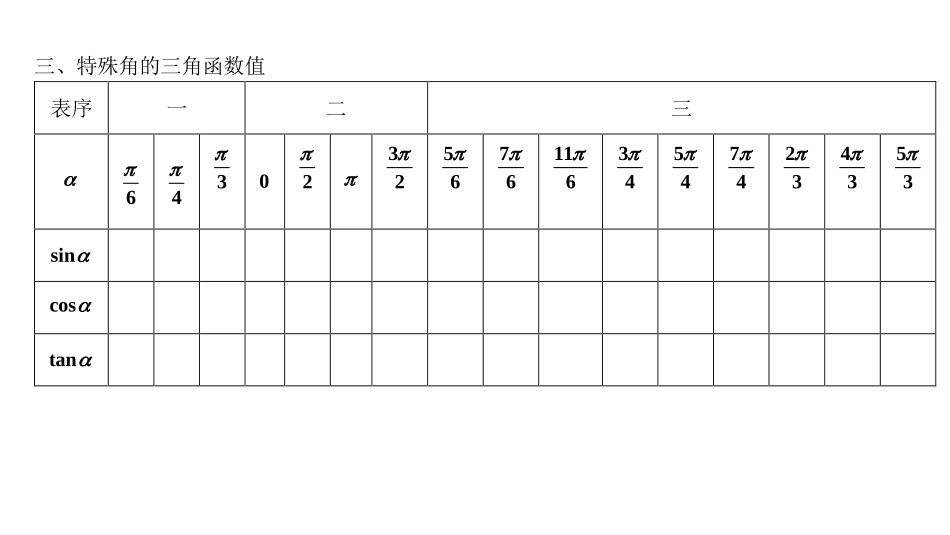
一、同角三角函数关系平方关系:商数关系:二、诱导公式口诀奇变偶不变，符号看象限（奇数2时名称要变，偶数2时名称不变）函数名不变，符号看象限正余名互变，符号看象限角2k（kZ）223232sincostan【说明】用诱导公式求(或化简、比较)数值角的三角函数值的大小时，口诀是“负化正，大化小，化到锐角就行了”。特殊角的三角函数值要用数值作答。三、特殊角的三角函数值表序一二三64302325676116345474234353sincostan解析式sinyxcosyxtanyx图象定义域值域最值最大值最大值无最大值和最小值最小值最小值奇偶性周期性TTT单调性增区间增区间增区间减区间减区间对称性对称中心为（）对称中心为（）对称中心为（）对称轴为x对称轴为x解析式sinyxcosyxtanyx图象五、sin()yAx的图象与图象变换()kZ（一）sin()yAx的五点作图法项目三角函数sin()yAx（0A，0）图象作法列表描点法：“叁零两最”五点法待定坐标法x02322先从上升段零点开始作一个周期的图象，后写出“叁零两最”五个关键点的坐标。最后作出y轴并标上A和A。x1x2x3x4x5xy010-10（二）图象变换（口诀：左加右减）sinyx→sin()yAx注意：两种途径平移时的平移量不同。方法一：先平移，后伸缩方法二：先伸缩，后平移先将sinyx向__平移__个单位；再将图象上的点___坐标不变，坐标__变为原来的___倍。先将sinyx上的点坐标不变，坐标变为原来的___倍；再将图象向___平移___个单位。两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=tanAtanB-1tanB+tanAtan(A-B)=tanAtanB1tanBtanA倍角公式sin2A=2sinA•cosAcos2A=cos2A-sin2A=2cos2A-1=1-2sin2Atan2A=Atan12tanA2其它公式a•sina+b•cosa=)b(a22×sin(a+c)(其中tanc=ab)正弦定理RCcBbAa2=sin=sin=sin(R为三角形内切圆半径)余弦定理Cabbaccos2+=222