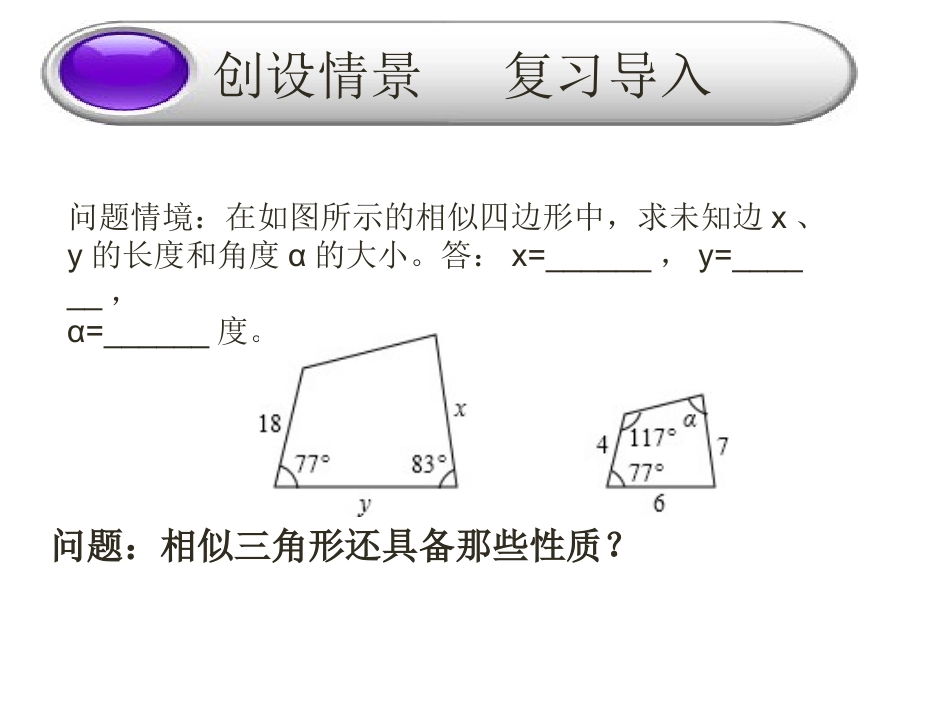
问题:相似三角形还具备那些性质?创设情景复习导入问题情境:在如图所示的相似四边形中,求未知边x、y的长度和角度α的大小。答:x=______,y=______,α=______度。导新定向1、理解掌握相似三角形对应线段(高、中线、角平分线)的比与相似比之间的关系2.运用性质解决实际问题自学思考题:1.相似三角形对应线段的比与相似比之间的关系2.如何证明上面的对应关系3.如何理解相似三角形对应线段4.完成下面的练习学教新课疑探交流根据上面的问题,结合自学效果,出现问题首先小组对议,较难的问题小组组议自学练习A′B′C′D′ABCD如图AD、A′D′分别是锐角△ABC和锐角△A′B′C′的中线,且△ABCA′B′C′,∽△则AD:A’D’=AB:A’B’.∵△ABCA′B′C′,∽△∴∠B=∠B’又因为AD、A′D′分别是△ABC和△A′B′C′的中线∴在△ABD和△A′B′D′中∴△ABDA′B′D′,∽△∴AD:A’D’=AB:A’B’.小组展示AB:A’B’.=BC:B′C′BD=0.5BCB’D’=0.5B′C′AB:A’B’.=BD:B’D’小组展示变式.如图AD、A′D′分别是锐角△ABC和锐角△A′B′C′的角平分线,且△ABCA′B′C′,∽△则AD:A’D’=AB:A’B’.ABCDA′B′C′D′小组展示你还能找到△ABCA′B′C′∽△的一组对应线段吗,他们与相似比有什么关系?ABCDA′B′C′D′文字语言:文字语言:相似三角形对应线段的比值等于相似比相似三角形对应线段的比值等于相似比符号语言∵AD、A′D′分别是锐角△ABC和锐角△A′B′C′的对应线段,且△ABCA′B∽△′C′,∴AD:A’D’=AB:A’B’.4。如图所示,有一块三角形余料△ABC,它的边BC=80cm,高AD=60cm.现在要把它加工成长与宽的比为2:1的矩形零件PQMN,要求一条长边在边BC上,其余两个顶点分别在边AB,AC上.求矩形的长和宽.变式:如图所示,有一块三角形余料△ABC,它的边BC=80cm,高AD=60cm.现在要把它加工成矩形零件PQMN,要求一条长边在边BC上,其余两个顶点分别在边AB,AC上.(1)矩形PQMN的边MN为何值时矩形面积最大(2)若矩形PQMN是正方形则求正方形的边长当堂检测1,本节课我有什么收获?2,通过本节课的学习我有什么感想?3,你对自己今天的表现满意吗?我反思我进我反思我进步步