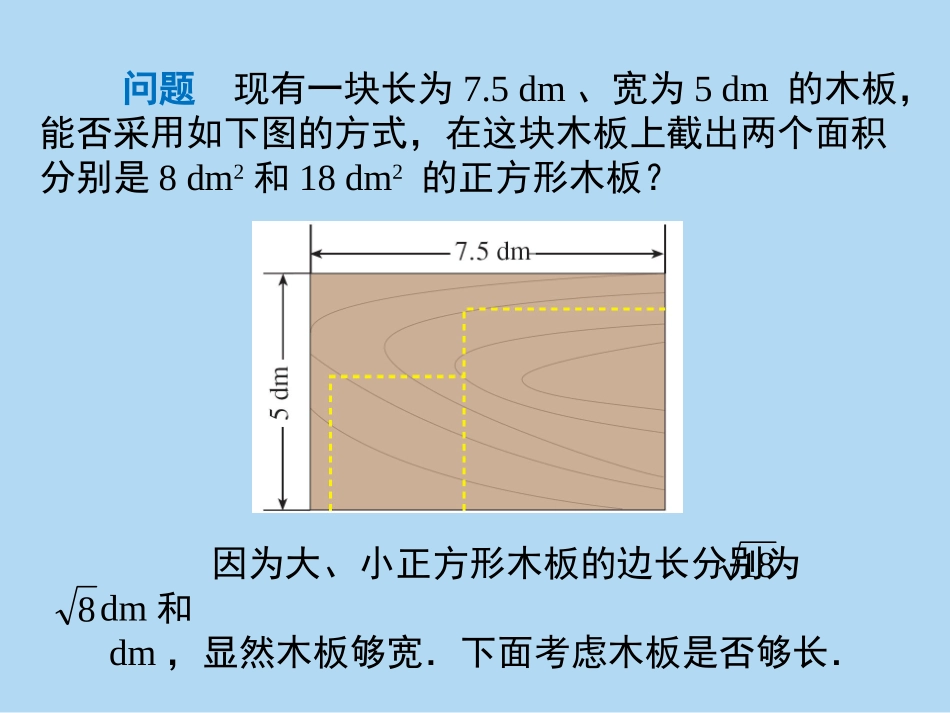
16.3二次根式的加减教学目标1.理解和掌握二次根式加减的方法.2.会进行二次根式的加减运算.教学重点二次根式化简为最简根式.教学难点会判定是否是最简二次根式.问题现有一块长为7.5dm、宽为5dm的木板,能否采用如下图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?因为大、小正方形木板的边长分别为dm和dm,显然木板够宽.下面考虑木板是否够长.188由于两个正方形的边长的和为()dm.这实际上是求,这两个二次根式的和,我们可以这样来计算:188188188.252322(化成最简二次根式)2)32((分配律)由<1.5可知<7.5,即两个正方形的边长的和小于木板的长,因此可以用这块木板按要求截出两个面积分别是8dm2和18dm2的正方形木板.252分析上面计算的过程,可以看到,把和化成最简二次根式后,由于被开方数相同(都是2),可以利用分配律将进行合并.1888182322和2322和一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.例1计算:aaaa53259(2);4580(1)解:53544580(1);5.259aa(2)8.a例2计算:;483313122(1)).53()2012((2)解:3123234483316122(1);314535232)53()2012((2).533练习答案1.(1)不正确,不能化简;(2)不正确,不能化简;(3)正确.2.(1)-4;(2)3;(3)10-3;(4)10+.3.0.83.24175236例3计算:;6)38((1).22)6324((2)解:63686)38((1);233463682263222422)6324((2).3232例4计算:;))52(32((1)(53(53).)(2)解:152523)2()52(32(2)(1);22131522222)3()5()35(35()(2).235练习答案1.(1)+;(2)4+2;(3)11+5;(4)4.2.(1)9;(2)a-b;(3)7+4;(4)24-4.65310102本章知识结构图再见!