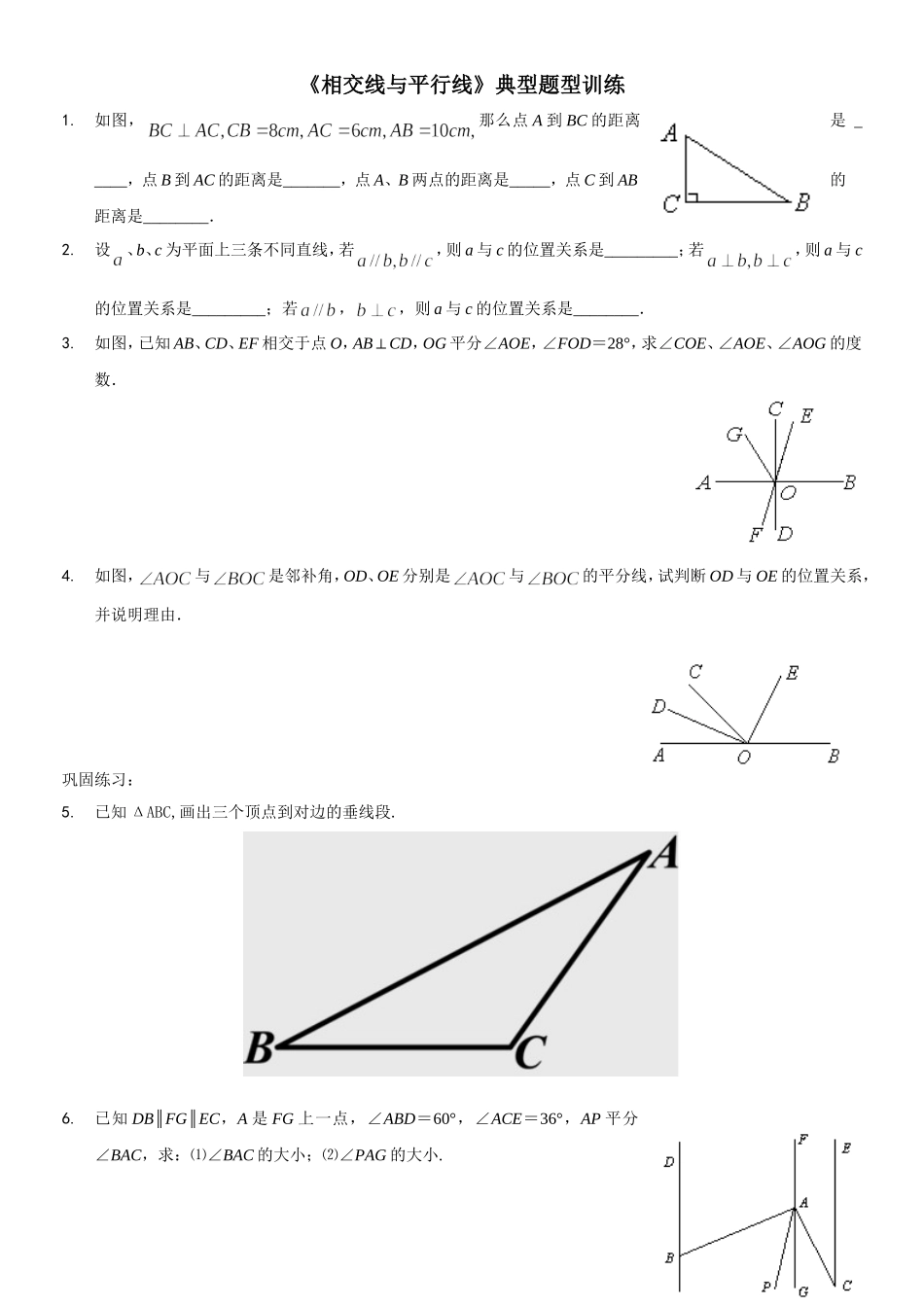
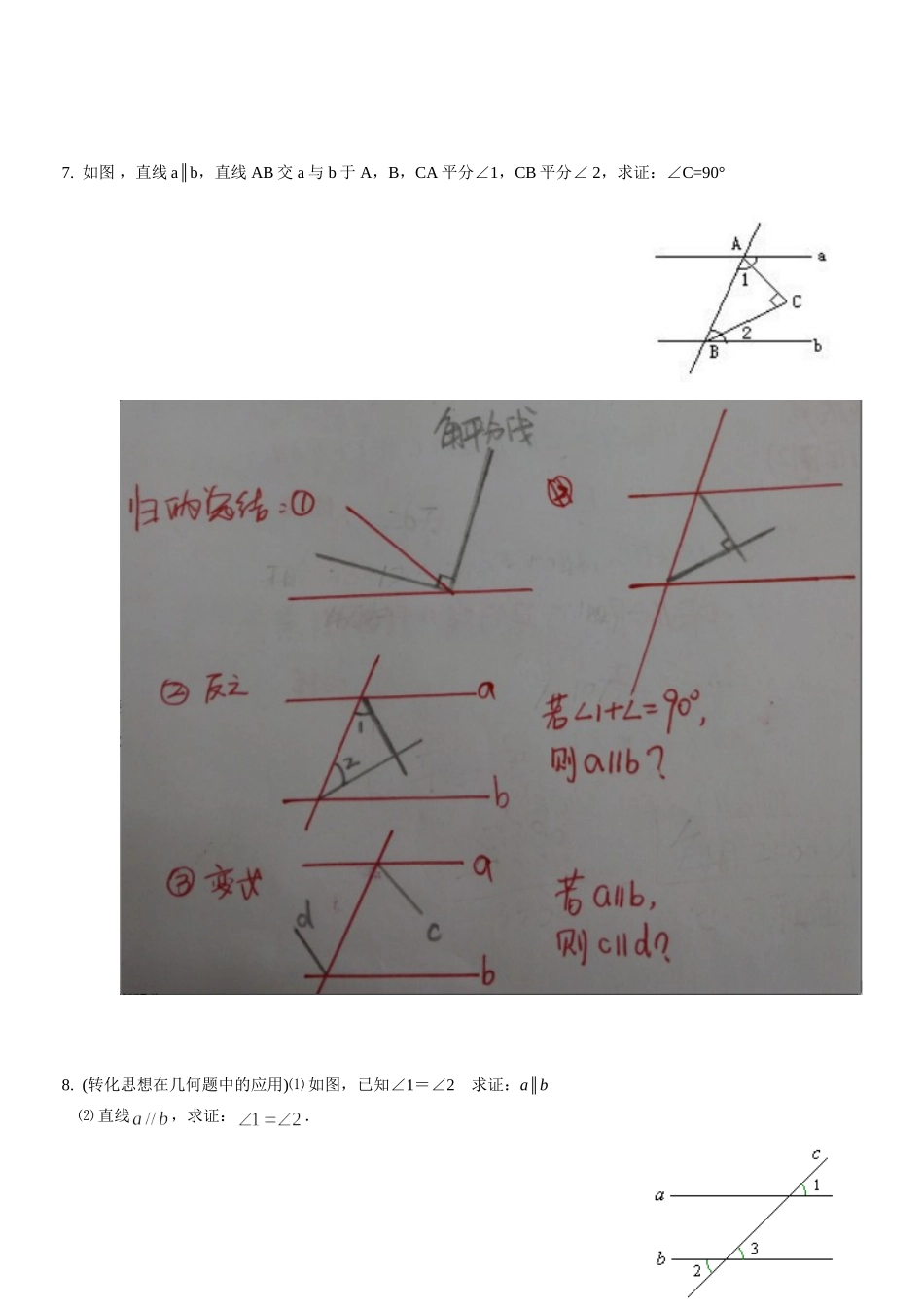
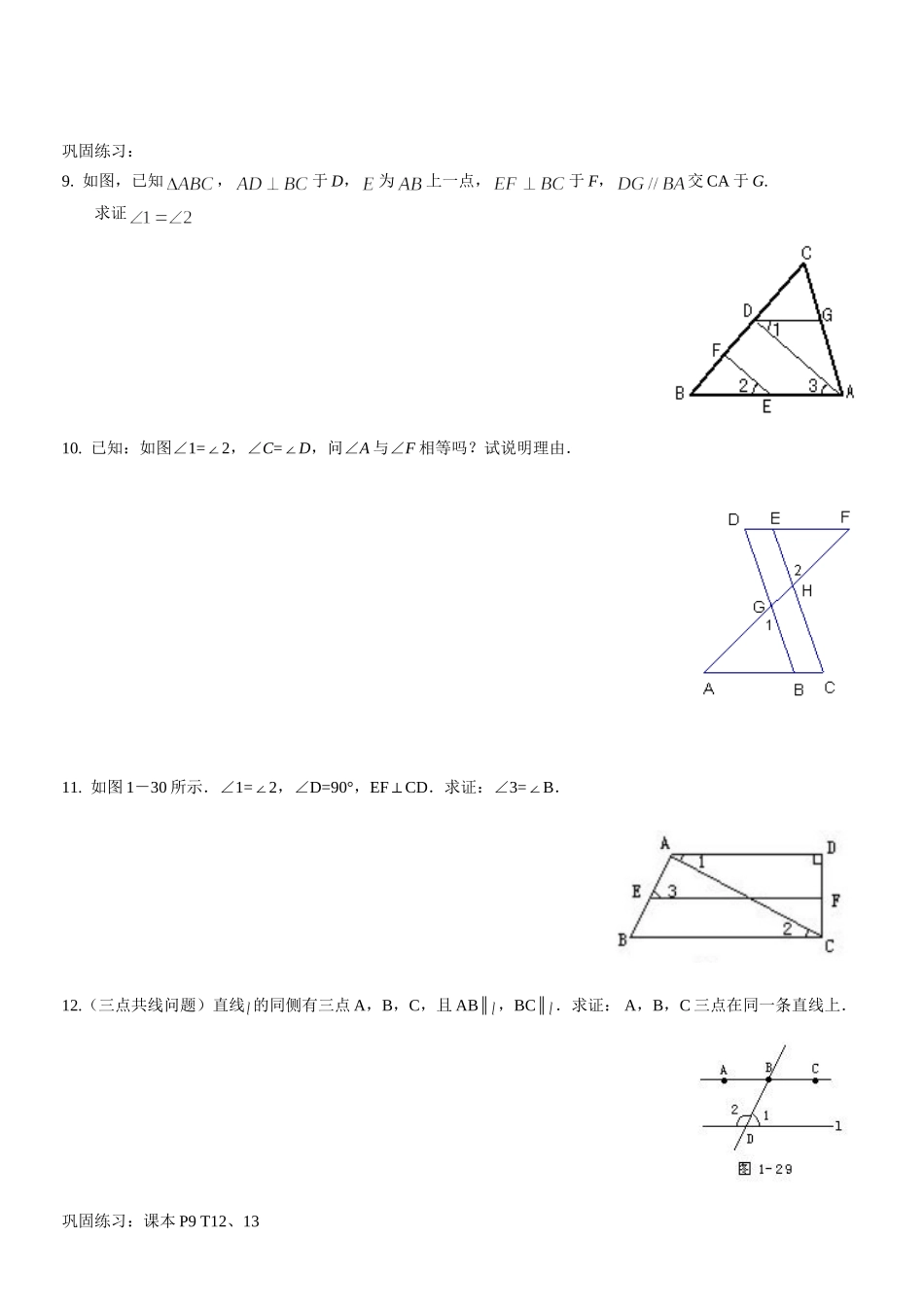
《相交线与平行线》典型题型训练1.如图,那么点A到BC的距离是_____,点B到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.2.设、b、c为平面上三条不同直线,若,则a与c的位置关系是_________;若,则a与c的位置关系是_________;若,,则a与c的位置关系是________.3.如图,已知AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度数.4.如图,与是邻补角,OD、OE分别是与的平分线,试判断OD与OE的位置关系,并说明理由.巩固练习:5.已知ΔABC,画出三个顶点到对边的垂线段.6.已知DB∥FG∥EC,A是FG上一点,∠ABD=60°,∠ACE=36°,AP平分∠BAC,求:⑴∠BAC的大小;⑵∠PAG的大小.7.如图,直线ab∥,直线AB交a与b于A,B,CA平分∠1,CB平分∠2,求证:∠C=90°8.(转化思想在几何题中的应用)⑴如图,已知∠1=∠2求证:a∥b⑵直线,求证:.巩固练习:9.如图,已知,于D,为上一点,于F,交CA于G.求证10.已知:如图∠1=2∠,∠C=∠D,问∠A与∠F相等吗?试说明理由.11.如图1-30所示.∠1=2∠,∠D=90°,EFCD⊥.求证:∠3=B∠.12.(三点共线问题)直线的同侧有三点A,B,C,且AB∥,BC∥.求证:A,B,C三点在同一条直线上.巩固练习:课本P9T12、1313.(阅读理解题)如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.解:∠B+∠E=∠BCE过点C作CF∥AB,则()又∵AB∥DE,AB∥CF,∴____________()∴∠E=∠()∴∠B+∠E=∠1+∠2即∠B+∠E=∠BCE.14.阅读理解并在括号内填注理由:如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.证明:∵AB∥CD,∴∠MEB=∠MFD()又∵∠1=∠2,∴∠MEB-∠1=∠MFD-∠2,即∠MEP=∠______∴EP∥_____.()