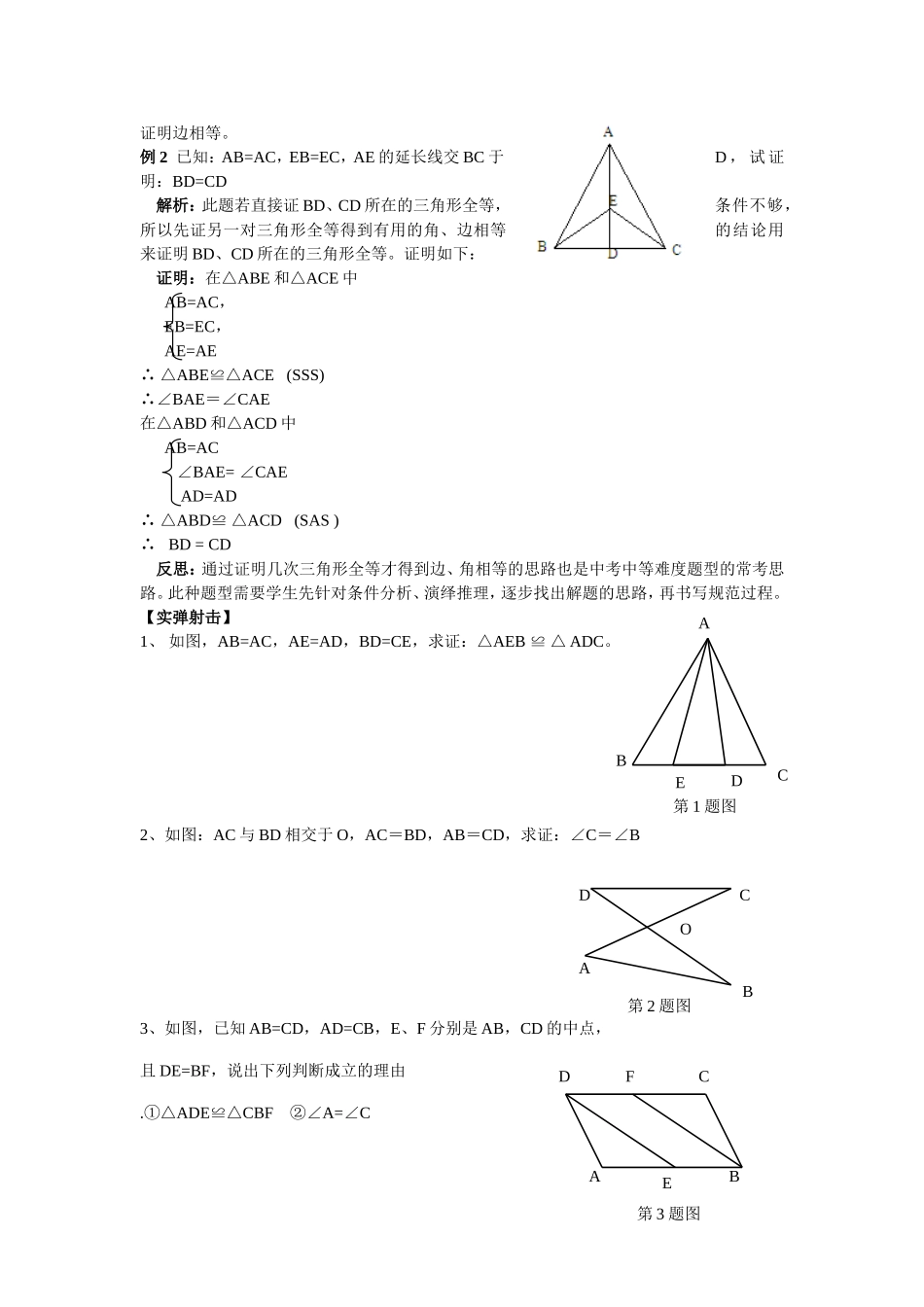
全等三角形【复习要点】1、全等三角形的概念:能够完全的两个三角形叫做全等三角形。2、全等三角形的性质:全等三角形的对应边,对应角,全等三角形的对应中线,对应高,全等三角形的对应角平分线。全等三角形的面积,周长。3、全等三角形的判定:一般三角形边角边(SAS):有两条边和它们的夹角对应相等的两个三角形全等角边角():有两个角和它们的夹边对应相等的两个三角形全等角角边():有两角和其中一角的对边对应相等的两个三角形全等边边边():三边对应相等的两个三角形全等直角三角形两条直角边对应相等(SAS)一边一锐角对应相等(或)斜边、直角边对应相等()(二)实例点拨例1(2010淮安)已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE。求证:AE=BD。解析:此题可先证三角形全等,由三角形全等得出对应边相等即结论成立。证明如下:证明:∵点C是线段AB的中点∴AC=BC∵∠ACD=∠BCE∴∠ACD+∠DCE=∠BCE+∠DCE即∠ACE=∠BCD在△ACE和△BCD中,AC=BC∠ACE=∠BCDCE=CD∴△ACE≌△BCD(SAS)∴AE=BD反思:证明两边相等是常见证明题之一,一般是通过发现或构造三角形全等来得到对应边即要证边相等,或者若要证边在同一个三角形中,也常先证角相等,再用“等角对等边”来EBCAD证明边相等。例2已知:AB=AC,EB=EC,AE的延长线交BC于D,试证明:BD=CD解析:此题若直接证BD、CD所在的三角形全等,条件不够,所以先证另一对三角形全等得到有用的角、边相等的结论用来证明BD、CD所在的三角形全等。证明如下:证明:在△ABE和△ACE中AB=AC,EB=EC,AE=AE∴△ABE≌△ACE(SSS)∴∠BAE=∠CAE在△ABD和△ACD中AB=AC∠BAE=∠CAEAD=AD∴△ABD≌△ACD(SAS)∴BD=CD反思:通过证明几次三角形全等才得到边、角相等的思路也是中考中等难度题型的常考思路。此种题型需要学生先针对条件分析、演绎推理,逐步找出解题的思路,再书写规范过程。【实弹射击】1、如图,AB=AC,AE=AD,BD=CE,求证:△AEB≌△ADC。2、如图:AC与BD相交于O,AC=BD,AB=CD,求证:∠C=∠B3、如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠CCABDE第1题图OACDB第2题图ADBCFE第3题图4、已知:BECF在同一直线上,AB∥DE,AC∥DF,并且BE=CF。求证:△ABC≌△DEF5、(09湛江)如图,AB是O⊙的切线,切点为BAO,交O⊙于点C,过点C作DCOA,交AB于点D.(1)求证:CDOBDO;(2)若30AO°,⊙的半径为4,求阴影部分的面积.(结果保留π)6、(09梅州)已知:如图,直径为OA的M⊙与x轴交于点OA、,点BC、把OA分为三等份,连接MC并延长交y轴于点(03)D,.(1)求证:OMDBAO△≌△;(2)若直线l:ykxb把M⊙的面积分为二等份,求证:30kb.yxCBAMO421303D,(第6题图)OABCD第5题图FEDCBA第4题图